In the image below, rays of light are hitting the GRIN (Gradient-index) lens at the optical angle and then converge towards the optical axis. Why do they do this? The refractive index is only a function of the distance from the optical axis and the rays of light are all parallel to that. Without a change in refractive index, the rays of light should not change direction (Snell's law).
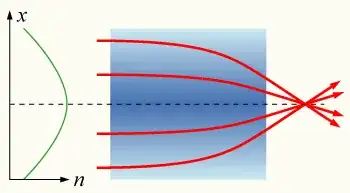
In a medium with varying refractive index $n(x,y)$ the differential equations for the ray curve point $(x,y)$ are as follows1:
$$\begin{align} \frac{\partial n}{\partial x}&=\frac{\mathrm d}{\mathrm{d}s}\left(n\frac{\mathrm{d} x}{\mathrm{d} s}\right),\\ \frac{\partial n}{\partial y}&=\frac{\mathrm d}{\mathrm{d}s}\left(n\frac{\mathrm{d} y}{\mathrm{d} s}\right), \end{align}$$
where the parameter $s$ is the path along the ray.
If we take the refractive index to vary along $y$ but remain constant along $x$, e.g.
$$n(x,y)=1+ay,$$
and then try to substitute what we think to be the solution for $y$-coordinate of the ray,
$$y(s)=y_0,$$
we'll find that the second equation reads
$$a=0.$$
In other words, this solution is only valid for vacuum, not for any linear-index material. Similar results will be for quadratic profile of refractive index. Thus, the ray must curve, not propagate in straight line.
If you try instead $n(x,y)$ piecewise-constant in $y$, you'll find that rays can indeed propagate along the constant-index strips, so this doesn't contradict Snell's law. It's just that Snell's law doesn't work at the boundary, and in the limit of smooth refractive index profile all points will be boundaries.
References
1: Kevin Brown, "Reflections on Relativity", §8.4 "Refractions on Relativity". Relevant derivation is quoted in my answer to How to calculate the refracted light path when refraction index continuously increasing?
Light waves travel in a direction perpendicular to the wave front. When a plane wave is incident at the left-hand face of the GRIN lens in the diagram you provided, the speed of the wavefront propagation increases with radial distance from the axis of the lens. As a result, the wave front is deformed into a concave, spherical wavefront -- same as what happens with an ordinary lens. The spherical wavefront converges to a focus because it propagates in the perpendicular direction, toward the center of curvature of the wavefront.
To get you started, consider that Maxwell’s equations are for the divergences and curls of the fields. These quantities are not strictly local in the sense that they are sensitive to what the fields are doing nearby, because they are derivatives in space. With this in mind, perhaps it is a little more intuitive why the rays might bend, even though they initially travel perpendicular to the gradient.
