Weight Distribution of a Heap of Logs

Question

Suppose that you have a heap of logs. Each log is the same length $l$, the same mass $r$ , and the same radius $r$. For simplification, their rotational inertia is $I=\frac{1}{2}mr^2$, their coefficient of static friction with the ground is $\mu_g$, and with each other is $\mu_l$. Suppose we stack them in $n$ layers, with $n$ logs on the bottom, $n-1$ logs on the next layer, $n-2$ on the next, et cetera until the top row has $1$. I have made a diagram depicting a 4 layer log pile, shown below.

My overall goal is to find what values of $\mu_g$ and $\mu_l$ are required for stability. In order to do that, I would like to find the net downward force on the bottom logs. I am pretty sure we could model the entire system of logs with individual net force and torque equations, and solve for the relevant variables, but this way of finding the force is extremely unwieldy and time-consuming. However after a little bit of thinking, I began to hypothesize an easier way to do find it.

If I split the stack into two sections, the bottom layer and the rest of the stack, the rest of the stack forms a new, smaller stack itself. Additionally, taking the stack as a whole, the total net force downward is simply their weights summed together.

Therefore, my question is can I divide this net force evenly from the upper part of the stack among the contact points with the bottom layer to find each of their net downward forces? If not, why not? If so, how do I divide it?

Answer 1

Someone correct me if I'm wrong, but I think I finally arrived at an answer.

It turns out that we actually can distribute the weight in the way I have described (by evenly dividing the total weight of the pyramid by the points of contact) by exploiting the symmetry present in the situation. Let's examine a simple three log case, without any friction between the logs. I have created a free body diagram shown below:

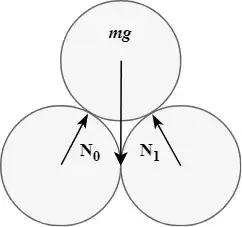
The only forces present on the top log is $mg$ pointing down, and $N_0$ and $N_1$ pointing up and inward. We can represent this situation as the system of equations

$$\Sigma F_x=N_{0x}-N_{1x}=0$$$$\Sigma F_y=N_{0y}+N_{1y}-mg=0$$

• Since the two normal forces are of equal angle, we can re-arrange the first equation to become $N_0 = N_1$.
• Using this information, we can re-arrange the second equation to arrive at $N_{0y}=N_{1y}=\frac{1}{2}mg$.
• This means that along the directions of $N_0$ and $N_1$, a downward force of $\frac{1}{2} mg$ is applied. For this situation, that means the downward force in the y-direction of the bottom two logs is $\frac{1}{2} mg + mg=\frac{3}{2}mg$, which is indeed the total weight of the pyramid divided by the contact points.

Now, this proves the case for a simple 3 log pyramid, but we must also consider pyramids with a larger amount of logs. Consider a 6 log pyramid. A diagram is shown below:

Let's consider the bottom and middle layers. Applying the same logic as above, we can solve for the downward force of the bottom layer.

• From left to right, so far it's $\frac{3}{2}mg$, $2mg$, $\frac{3}{2}mg$.
• However, let's now take into account the topmost log. The topmost log applies a force of $\frac{1}{2}mg$ straight down in the direction of $N_0$ and $N_1$.
• Since the middle balls lie directly in the path of this direction, the force travels straight through them, into the bottom layer. This only happens because we are dealing with an ideal pyramid.
• With this additional downward force applied only to the left and right logs, we arrive at the conclusion that the downward force on the each of the bottom logs is $2mg$, which is indeed the total weight divided by the contact points.

With this logic in hand, we can apply this idea to bigger and bigger pyramids, coming to the same conclusion. So yes, you can indeed find the net downward force on a bottom log by dividing the total weight of the pyramid by the number of contact points!

---

Now, the question remains, what if we add torque back into the equation?

Well after doing some research, I found this lovely person on the internet, wltrup, who solved this same problem for the two layer case. He found the same result, $\frac{3}{2}mg$ for the downward force on the bottom two logs even with torque. This makes sense, as the frictional forces within the pyramid all point perpendicularly to the normal forces, thus not "eating them up" so to speak. Thus, using the logic above, we can generalize this statement to situations even with torque!