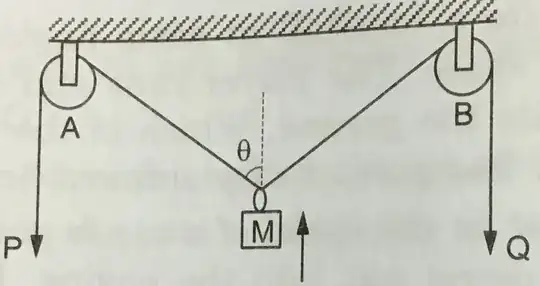
In general these kinds of problems with pulleys are solved in the same way, so I'll provide an explanation so it's useful for others.
First, note that the length of the string is constant, and denote it by $L$. Now, let's divide it in four segments:
$$L=L_A+L_{m,left}+L_{m,right}+L_B=constant$$
From the geometry of the figure, you may want to express the other lengths in function of known quantities.
Now if we take the derivative of the above expression,
$$v_A+v_{m,left}+v_{m,right}+v_B=0$$
Since you're interested in the upwards velocity, from the geometry of the problem you can clearly see that,
$$v_y=v_{m,left}\cos\theta=v_{m,right}\cos\theta$$
Substituting,
$$v_A+2v_y\cos\theta+v_B=0$$
Since the problem says the segments $A$ and $B$ are moving downwards, then $v_A=v_B=-u$, so we finally get:
$$v_y=u\cos\theta$$
You were on the right track, however I think you got confused with the trigonometric identities, hence why you got the cosine on the wrong position.