1

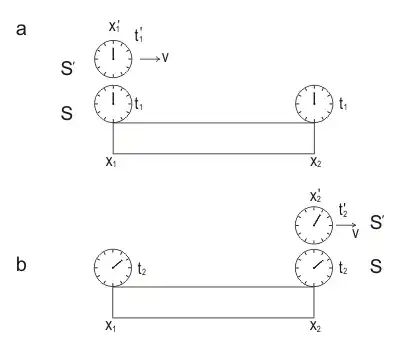
enter image description here Let's say we have an observer named Jack on a spaceship traveling at a constant velocity of 0.95c to the right, according to Bill, who is on the Earth. Then the spaceship reaches planet A and then planet B and keeps moving at constant velocity. The spaceship NEVER accelerates. The 2 events in this problem is Event 1, which is Jack meeting planet A, and Event 2, which is Jack meeting planet B. We give Jack and Bill each a clock and we want to compare the time elapsed between the 2 events that Jack records and the time elapsed between the 2 events that Bill records. My teacher said that Bill records more time for the A to B journey because this is basically the twin paradox. But I disagreed because the problem doesn't involve any acceleration. My argument was that Bill records more time because it's impossible for a single clock at rest relative to Bill to be at the position of Event 1 and at the position of Event 2. However, you CAN have a clock at rest relative to Jack that is at Event 1's position AND Event 2's position. This is the very definition of proper time: time measured by a clock whose position is at the position of both events. Proper time is the shortest measured time, so Bill records more time not because of the twin paradox but because ONLY Jack records the proper time, or shortest time, for these 2 events. Am I correct in my thinking?

EDIT:

enter image description here

I think I'm getting confused by exactly what the red clock that I circled represents. If we treat the green clock as the time measured by Bill and we choose to have Bill be stationary, the red clock can't represent the time Jack actually measures in his frame then. Rather, the red clock represents the time that Bill THINKS is elapsing for Jack?

  • Don't forget that in Jack's frame the distance AB is length-contracted relative to the distance in Bill's frame. – PM 2Ring May 23 '19 at 06:20
  • Red clock is a clock in immediate vicinity to Jack. Green clocks are synchronized clocks of Bill's frame. Inertial clock passes by and never returns. Hence, if Jack thinks that he is at rest, he needs another synchronized with his own clock at some distance. Then he can compare readings of Bill's clock with his own ones at different moments of time, to compare readings when Bill's clock passes by in immediate vicinity with any clock of Jack's rest frame. Jack's rest frame is a set of red synchronized clocks, Bill's rest frame is a set of green synchronized clocks. –  May 23 '19 at 08:56
  • Wait but the moving clock's time is not the time that the moving observer is actually experiencing right? –  May 23 '19 at 09:07
  • Because if we want to know the time the moving observer he or herself is actually experiencing, then we would have to make that moving observer the stationary observer. –  May 23 '19 at 09:09
  • So I guess the big mistake I'm making is that I think you can compare the time experienced by one observer with the time experienced by another observer. But you can't because you would have to set both observers as stationary which is impossible. The key word here is "experienced" i think –  May 23 '19 at 09:12
  • Right. He turns himself into "stationary" by means of filling space around him with synchronized clocks. What is In SR an observer never thinks about himself as about "moving one". He always points his finger at another guy and says that that guy is moving, but not himself. Another person or clock is moving in his frame and and changes spatial position in his frame. –  May 23 '19 at 09:13
  • Like in other words, I'm trying to have 2 different perspectives exist at the same time but thats not possible –  May 23 '19 at 09:13
  • Single clock lags behind many clocks. You can't compare single clock to single clock. Single clock is moving in a reference frame and its time runs slower than time in the WHOLE this rest frame. Time in the WHOLE rest frame runs faster then. Then a moving observer changes frame and introduces a set of his own clocks. Now he is at rest, and any moving clock lags behind his own one. Hocus pocus. Nobody think that he is moving and nobody thinks that he himself changes spatial position in someone's frame. –  May 23 '19 at 09:17
  • Let us continue this discussion in chat. –  May 23 '19 at 09:20
  • Why? All processes in his body slow down. All processes in his laboratory slow down. He feels nothing special. –  May 23 '19 at 09:20

2 Answers2

1

Singe "moving" clock always measures shorter time interval than two spatially separated and Einstein – synchronized clock.

A set of spatially separated and synchronized clocks (these clocks are at rest relatively to each other) represents a rest frame of an observer

By means of these synchronized clocks a "stationary" observer may know time of any event in any location of his frame. It makes sense to refresh a notion of “stationary observer”.

In your case Bill is "subjectively" at rest, and clocks A, B, E are at rest relatively to him, they are (I believe) Einstein – synchronized and show the same time. These clocks represent Bill's rest frame.

Jack is moving, i.e. changes his spatial position in Bill’s frame. If he compares his clock readings with clock A and B successively, he will see, that his clock measures shorter time interval, i.e. time in Bill’s rest frame runs faster than his own. However, Jack can change his status from “moving” one into “stationary” by means of changing frame. In this case he places at least one another clock at some distance and synchronizes this clock with that on his wrist.

In this case, if he employs Einstein’s synchronization procedure, assuming that the one -way speed of light is c, single Bills’s clock will measure shorter time interval than two synchronized Jack’s clocks.

Let us demonstrate time dilation of the SR in the following experiment (Fig. 1). Moving with velocity $v$ clocks measure time $t'$. The clock passes past point $x_{1}$ at moment of time $t_{1}$ and passing past point $x_{2}$ at moment of time $t_{2}$.

At these moments, the positions of the hands of the moving clock and the corresponding fixed clock next to it are compared.

enter image description here enter image description here

Let the arrows of moving clocks measure the time interval $\tau _ {0}$ during the movement from the point $x_ {1}$ to the point $x_ {2}$ and the hands of clocks 1 and 2, previously synchronized in the fixed or “rest” frame $S$, will measure the time interval $\tau$. This way,

$$\tau '=\tau _{0} =t'_{2} -t'_{1},$$

$$\tau =t_{2} -t_{1} \quad (1)$$

But according to the inverse Lorentz transformations we have

$$t_{2} -t_{1} ={(t'_{2} -t'_{1} )+{v\over c^{2} } (x'_{2} -x'_{1} )\over \sqrt{1-v^{2} /c^{2} } } \quad (2)$$

Substituting (1) into (2) and noting that the moving clock is always at the same point in the moving reference frame $S'$, that is,

$$x'_{1} =x'_{2} \quad (3)$$

We obtain

$$\tau ={\tau _{0} \over \sqrt{1-v^{2} /c^{2} } } ,\qquad (t_{0} =\tau ') \quad (4) $$

This formula means that the time interval measured by the fixed clocks is greater than the time interval measured by the single moving clock. This means that the moving clock lags behind the fixed ones, that is, it slows down.

The animation below demonstrates change of frames and time dilation:

enter image description here

0

But who is actually moving and who is actually stationary? You know that, according to Jack's frame of reference, the planets are rushing towards him with $v=-0.95c$.

AWanderingMind
  • 1,551