In Special Relativity, is it allowed to ask 'How much time has elapsed in a second inertial frame at a particular moment in the first inertial frame'?

Question

Or is it a meaningless question?

For example, A and his friend B are the same age initially. B travels relative to A at a very high speed. A keeps observing B from his frame. At one moment, A observes that B has aged only half as himself (say A is aged 60 when he makes the observation and observes B to be 30).

The question is 'How old is B from his own (B's) frame of reference at the moment A made the above observation?' If it has an answer, what is it? If the question is meaningless, why?

Answer 1

I really wish more books used spacetime diagrams to teach relativity, because 90% of confusion in relativity problems can be resolved by drawing a careful spacetime diagram. The idea is to superimpose the $t$ and $x$ axes for one observer (call them observer B) and the $t'$ and $x'$ axes for a moving observer (observer A) on the same diagram. All events that happen "at the same moment" according to observer B lie along a line parallel to the $x$-axis; all events that happen "at the same moment" according to observer A lie along a line parallel to the $x'$-axis.

Instead of 30 and 60 years, let's use 1 year and 2 years.¹ You ask

At one moment, A observes that B has aged only half as himself (say A is aged 60 when he makes the observation and observes B to be 30). How old is B from his own (B's) frame of reference at the moment A made the above observation?

The event we are concerned with in this case (i.e., the point on the spacetime diagram) is the event at which A observes B's age. The key ambiguity in this question is whether "at the moment" means "at the same moment" according to A, or "at the same moment" according to B. If 2 years have elapsed on A's clock when they measure B's age, then "at the moment of the observation" according to A, only 1 year has elapsed:

But "at the moment of the observation" according to B, 4 years have elapsed:

The fact that we need to draw different lines to "read off" $t$ and $t'$ is what makes the question a bit ambiguous as stated.

So (returning to the original numbers) to get an unambiguous answer, you can ask either

What is the $t$ coordinate (i.e. the time elapsed as observed by B) of the event where A observes B's age?

in which case the answer is 120 years. Or you can ask

What is the $t'$ coordinate (i.e. the time elapsed as observed by A) of the event where A observes B's age?

in which case the answer is 30 years. So long as you're clear about whether you want to know $t$ or $t'$, there is an unambiguous answer.

---

¹ This is largely so I can use some Mathematica code I already had on hand.

Answer 2

'How old is B from his own (B's) frame of reference at the moment A made the above observation?'

Your problem lies in the very moment you are talking about. In SR there isn't an unique moment for universe. A moment will be meaningful only if you specify your refrence frame of that moment.

i.e you should have asked something like this:

1.'How old is B from his own (B's) frame of reference at the moment $t$ in B's frame where A made the above observation?'

Or

2.'How old is B from his own (B's) frame of reference at the moment $t'$ in A's frame where A made the above observation?'

The answer to these questions is quite different! Unfortunetly i can't go on without math to explain differences. If you understood what i am saying then you need not to continue reading, unless you are interested in math as well.

To use lorentz transformations, we need to define events in spacetime. Let's say that A and B clocks are synchronized at $t=t'=0$. B arranges his birthday party when he become 30y/o. So we can assign an event in spacetime for this party $E_1=(ct,x)=(c(30y),0)$, (B is at orgin of his frame so $x=0$). If we were to use Galilean transformation to analyze this event in A's frame we would get $E_1'=(c(30y),-v(30y))$, in other words, according to Newton himself A will be 30y/o when he observes B's birthday party. (One might argue that light travel time between observers is not considered here. well, it's simple. Because observers are fully aware of their distance, they can tell how much time it took for the light to travel. So A can tell you guys when B's birthday actually happened though A will recieve singal much later in reality). With Lorentz transformation however, we will get $E_1'=(c\gamma(30y),\gamma(-vt))$. i.e according to Einstein, A is much older than B, when he observers B's birthday. Now back to the question, here i can show you why it's meaningless to ask

'How old is B from his own (B's) frame of reference at the moment A made the above observation?'

to answer your question From analogy above, one might jump to conclusion that of course B would be 30y/o, because after all we assumed so!(just check how did i define $E_1$) on the other hand, one might use inverse Lorentz transformation for event $E_1'$ above to see that $E_1=(c\gamma^2(30y),\gamma(vt))$ (as it was done by @RogerJBarlow) and conclude that B will be 120y/o. How is it possible?! well its because the moment you are talking about is different for every observers. in fact, if you were to ask the first question, the first answer would be your solution. on the other hand if you were to ask second question, the second answer would be right.

Update: Note that inverse Lorentz transformation is $t=\gamma (t'+vx'/c^2)$. if you pick $x'$ from event $E_1'=(c\gamma(30y),\gamma(-vt))$ you will arrive at $t=t$ which is obvious because using two Lorentz transformation at the same time does not change anything. However, if you assume another event ("observing itself") in A's frame such that $E_1'=(ct',x')=(c\gamma(30y),0)$ ($x'=0$ because A is at his orgin) then you will get the second answer.

TL;DR

In B's point of view, the moment he become 30y/o is not simultaneous with the moment that A observes him. And no, It's not because of light travel time. So he conclude that when A observes him, he is 120y/o while what A observes is B 30y/o!

Answer 3

The outcome depends on the method, how A (or B) measures and which clock he compares to which clock.

The problem is that A and B can only directly compare readings of their clocks when they are at the same point. If they are at some distance from each other, to say what "another clock" shows they must make some assumptions about the one-way speed of light and put another clock that is synchronized with their own clock.

Let's at initial moment A and B are at “starting position" close to each other and the both their clocks show 0.

1) Let’s A is “at rest” and B is moving. A places clock A1 at starting point and clock A2 at finish and synchronizes these clocks by a beam of light, assuming that the one – way speed of light is c. When B comes to the clock A2 he compares readings (in immediate vicinity) of his own clock with the clock A2. The clock A2 shows 60, while the clock B shows 30.

2) Let’s B is “at rest” and A is moving. B places clock B1 at starting point and clock B2 at finish and synchronizes these clocks by a beam of light, assuming that the one – way speed of light is c. When A comes to the clock B2 he compares readings (in immediate vicinity) of his own clock with the clock B2. The clock B2 shows 60, while the clock A shows 30.

Let us demonstrate time dilation of the SR in the following experiment (Fig. 1). Moving with velocity $v$ clocks measure time $t'$. The clock passes past point $x_{1}$ at moment of time $t_{1}$ and passing past point $x_{2}$ at moment of time $t_{2}$.

At these moments, the positions of the hands of the moving clock and the corresponding fixed clock next to it are compared.

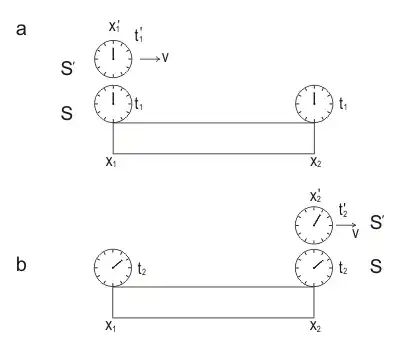
Let the arrows of moving clocks measure the time interval $\tau _ {0}$ during the movement from the point $x_ {1}$ to the point $x_ {2}$ and the hands of clocks 1 and 2, previously synchronized in the fixed or “rest” frame $S$, will measure the time interval $\tau$. This way,

$$\tau '=\tau _{0} =t'_{2} -t'_{1},$$

$$\tau =t_{2} -t_{1} \quad (1)$$

But according to the inverse Lorentz transformations we have

$$t_{2} -t_{1} ={(t'_{2} -t'_{1} )+{v\over c^{2} } (x'_{2} -x'_{1} )\over \sqrt{1-v^{2} /c^{2} } } \quad (2)$$

Substituting (1) into (2) and noting that the moving clock is always at the same point in the moving reference frame $S'$, that is,

$$x'_{1} =x'_{2} \quad (3)$$

We obtain

$$\tau ={\tau _{0} \over \sqrt{1-v^{2} /c^{2} } } ,\qquad (t_{0} =\tau ') \quad (4) $$

This formula means that the time interval measured by the fixed clocks is greater than the time interval measured by the single moving clock. This means that the moving clock lags behind the fixed ones, that is, it slows down.

Every observer repeats the same procedure.

The animation below demonstrates change of frames and time dilation:

Time of "stationary" observer is the same (universal) in the whole frame and evenly distributed across the whole frame. So, when some answers mean, that B is not younger, but surprisingly older, they are in some sense correct, because they mean time of the whole reference frame, in which A moves. The stationary observer "occupies" the whole frame. Time in the "stationary" reference frame B runs faster than the time of the single moving clock A; Time in the "stationary" reference frame A runs faster, than the time of the single moving clock B.

Answer 4

It's a little hard to interpret your quoted question: "How old is B from his own frame of reference at the moment A made the above observation?" I'm interpereting this to mean "According to B's frame of reference, how old is B at the moment when A makes his observation?" If you meant something else, then the following might not apply:

I'm assuming that when B left earth, both A and B were aged zero.

1) When A is 60, he says that B is 30. (This was given in your post.)

2) The situation is entirely symmetric, so when B is 60, he says that A is 30.

3) Therefore we know that A ages at half-speed in B's frame.

4) Therefore when B is 120, he says that A is 60.

5) A makes his observation when he is 60. Therefore when B is 120, he says "At this moment, A is making his observation".

So the answer to your question is 120, and since your question has an answer it is meaningful --- if you meant what I think you meant.

Answer 5

It's all in the Lorentz Transform: $t'=\gamma (t-v x/c^2)$

In your case $\gamma=2$, $t=60$ and as $A$ is presumably at the origin, $t'=120 $y, as @WillO says.

However different values of $x$ would give different $t'$. So this is not 'a particular moment in the first inertial frame' which is what your question asks about. At the $t=60$ moment there are presumably various events occurring simultaneously (!) according to $A$; $B$ will see them as having different $t'$ as they have different $x$ values.

Answer 6

Since the situation is symmetric there are 2 answers, one for each frame of reference. If we take the relative velocity to be v=0.866c for a gammafactor of γ=2, when A is 100 years old, in A's frame B is only 50 years old. In B's frame, when B is 50 years old, A is only 25 years old. If they could beam information to each other they could build an antitelephone with which they could send information into their own past (If A beams a message to B when A is 100 years old and B beams it back to A, A will receive his own message when he is 25 years old). Therefore faster than light information or beaming could cause causal violations.