5

There was a text book question in my physics class this morning on what happens to the strength of an electric field $E$, if its distance between two plates decreases by 2 fold.

My initial thought was, "Well, then the electric field would double!", this was because I was just introduced by this equation the prior week:

enter image description here

But the answer key says otherwise, with a graph included, enter image description here

the line is curved, which eliminates my though of $E$ being directly proportional to $d$. This confused me for quite a while. So I decided to browse for further clarification, one site told me that $E$ is inversely proportional to square of $d$, which confused me even more.

After a more in-depth research, I found another equation known as the Coulomb's law equation, which I'm pretty familiar with, but never knew there was an equation for it.

enter image description here

$r$ , which in this case, is equivalent to $d$, states that decreasing the distance $d$ by any value would increase $E$ by the power of it, which also follows the Inverse Square Law. So I made a few scenarios:

Case 1

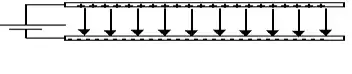
enter image description here

If I was to have 2 separate circuits, both containing 2 identical plates connected to a source, but with different distances, let's say $10 cm$, the other one by $20cm$. Leaving it untouched, the field strength ratio would be $2E:E$, (in accordance to $V=Ed$)

Case 2

enter image description here

I decided to make this GIF. for a better visualization. Assume that, initially, the distance $d$ between the 2 metal plates is $10cm$, which is then moved carefully to $20cm$. According to Coloumb's Law equation, the ratio of field strength initially ($10cm$) and after ($20cm$), would be $4E:E$.

Does it really happen in the real world, when the plates are in different configurations, it seems like they're following different equations? Nevertheless, this is the peak of my confusion, it seems that both equations are contradictive, which aren't supposed to be. What am I missing out on?

In addition, I also notice that $V=Ed$ only applies when there's a constant field. But WHY ? Why does that equation only work when there's a uniform electric field? Is there something to do with $V$ altering when $d$ or $E$ changes?

Any answer would be greatly appreciated!

Community
  • 1
  • I'm currently in High school, so please understand if there are some misunderstandings here and there as I'm relatively new on this topic. Any intuitive and concise answer would be very helpful. –  Jul 24 '19 at 14:10

4 Answers4

5

Lots of good questions here, and plenty of common misconceptions. I'll do my best to clear them up. The main thing to keep in mind is this:

Strictly speaking, Coulomb's Law only applies to point charges.

If you have a charge of magnitude $q$ concentrated at a single point, the electric field a distance $r$ from that charge has magnitude $$ E = \frac{kq}{r^2}. $$ The direction of this field is directly away from the charge if it's positive, and directly towards the charge if it's negative.

If you want to find the electric field at some point $P$ from any other object, you have to treat it like a collection of point charges. For example, you could imagine carving up both of your plates into a huge number of teeny-tiny chunks, each of which has a teeny-tiny amount of charge on it. You would then figure out what the electric field vectors from each one of these chunks is, and then you'd add together all of these vectors to find the total electric field at $P$. As you can imagine, this would be rather tedious, but you could do it in principle. The entire discipline of calculus was developed to solve problems like this, where you have to add up a large number of tiny contributions. Calculus is usually introduced in college/university-level physics classes, so that's something for you to look forward to.

This said, it works out that you can often apply Coulomb's law directly to charges that aren't just charges concentrated at a finite point. For example, suppose the charge $q$ is spread out on a perfect sphere of radius $R$. For any point $P$ where you want to find the field, some of the "chunks" are farther away (on the "far side" of the sphere), and some are nearer, and they don't all point in the same direction. But it turns out that if you add together all these contributions, the field is exactly the same as if the charge $q$ was all concentrated at one point at the center of the sphere.

Moreover, even if the charge isn't a perfect sphere, Coulomb's Law (while not exactly correct) often does a good enough job. For example, if I have the charge $q$ spread out on the surface of a peanut about 5 cm long, and I want to know the electric field due to this peanut at a distance of $r = 100$ m away, it turns out that the electric field is pretty close to $kq/r^2$. In effect, when you're really far away from an object, compared to its size, then you can treat the object as though all of its charge was concentrated at a single point.

So where does this fail for the plates?

In the case of the plates, you're assuming that you are much closer to the plates than the size of the plates. So you can't treat the plates like they're point charges (as you do in Case 2); the distance between the point $P$ and the plate is much smaller than the size of the plate itself.

Instead, it turns out (if you do that "carve-it-up-and-add-it-up" procedure that I mentioned above) that the electric field at a point near a uniformly charged plate is basically constant. By "near", I mean that the distance to the plate is much smaller than the size of the plate. It's also proportional to the amount of charge on the plates. Specifically, it turns out that for a large plate, we have $$ E \approx \frac{2 \pi k q}{A}, $$ where $A$ is the area of the plate.

So:

  • If we take two plates with a fixed amount of charge on them, and we move them farther apart (though not so far that the distance between them becomes comparable to their size), the electric field stays the same.

  • On the other hand, if we hook the plates up to a battery, then the battery wants to maintain a constant potential difference $V$ between the plates. Since $d$ is halved, the electric field doubles in this case. This means that the battery must pump some charge around in this process; otherwise, $V$ wouldn't stay constant. In particular, since $E$ has doubled, the battery must double the charge on each plate.

Community
  • 1
Michael Seifert
  • 48,772
  • So you're saying that decreasing the distance between the plates by half, would make E 2x larger? Shouldn't it be 4x? When I google "the relation between E and d, it states that it is inversely proportional to the square. I'm still pretty confused on why the E doubled –  Jul 25 '19 at 12:29
  • 1
    @KEVINN: There are two problems with just applying Coulomb's Law there. The first is that if a battery is connected, the charge on the plates isn't constant; the battery pumps some charge around. Second, the distance between the plates is not the same as the distance between a point $P$ where you're measuring the electric field $E$ and one of the plates. In fact, there isn't a well-defined "distance between $P$ and the plate"; some of the points on the plate are closer to $P$, and some of them are farther away. – Michael Seifert Jul 25 '19 at 20:54
  • Here's the link for the question that was shown on my class http://physics-ref.blogspot.com/2015/06/physics-9702-doubts-help-page-160.html its (No.798) –  Jul 26 '19 at 12:11
  • It's shown that the correct answer is (A), does graph A represents an Inverse Square Law curve? –  Jul 26 '19 at 12:14
  • I'm doubting the graph because, by observing, half-ing $d$ doesn't give us $4E$ –  Jul 26 '19 at 12:16
  • @KEVINN: I believe it's supposed to represent an inverse proportionality ($E \propto 1/d$), not an inverse square proportionality ($E \propto 1/d^2$). Since the plates are held at a constant potential difference, the electric field at a point between the plates is inversely proportional to the distance between them. This is due to the battery adding more charge to the plates to keep $V$ constant. – Michael Seifert Jul 26 '19 at 12:17
  • @KEVINN: I wouldn't get hung up on the exact shape of the graph, though. Questions like this are meant to test qualitative knowledge of how quantities depend on each other, not to represent precise quantitative relationships. – Michael Seifert Jul 26 '19 at 12:19
  • Let us continue this discussion in chat. – Michael Seifert Jul 26 '19 at 12:21
1

The reason that $V=Ed$ only applies when there is a constant field is that the voltage is actually the integral of the electric field with respect to distance.

$$V = \int_a^b \mathbf{E} \cdot \text{d}\mathbf{r}$$ If $\mathbf{E}$ is constant, you can pull it out of the integral and the result is just $V=|\mathbf{E}| (b-a) = E d$.

You can think of it like the electric field being the slope of a hill and the voltage being the change in height as you move from one point to the other on the terrain.

I'm pretty sure the answer from the answer key is for another problem. The graph shows the electric field going to infinity at distance $R$, but I don't see $R$ defined anywhere in the problem.

Vincent Thacker
  • 7,926
Hunter
  • 380
1

You know inverse square laws only work fine if the source is a point charge or a sphere which has charges uniformly distributed over it. You can apply the same analogy to masses also. Now coming to your question, voltage between two defined points

(remember, all voltages are relative, even the so called "absolute" voltage is taken relative to infinity)

is the amount of work required to move a charge across two points in a direction opposite to the direction of force without increasing the KE of the charge.

We know, $W=F\cdot d=Fd\cos\theta$ where $\theta$ is the angle between the direction of force and displacement. Let's assume that the movement of the charge always occurs in the direction of electrostatic force. In that case we'll just have

$W=Fd \tag1$

Also, this formula only works when the force over the entire distance moved is constant hence you'll have to integrate for cases like charged spheres and point charges. Since there exists a uniform E-field inside two charged plates, the force exerted is also the same.

Now we can re-write $(1)$ as $W=qEd \tag2$ where $F=qE$

Re-arranging, we have $\dfrac W q=Ed$ which is the definition of voltage we've just discussed. Now replacing $\dfrac W q$ by $V$ we have the required equation $$\boxed{V=Ed}$$

Remember, that only works for constant forces.

user8718165
  • 1,536
0

I think the biggest misconception that you make about the question is the graph of inverse relationship. The curved non linear graph does not necessarily correspond to 1/x^2, it might also be 1/x. So whether it is having a relationship as inverse or inverse with the square does not interfere with the question. Moreover, the graph of -x, nay a linear graph does not represent an inverse relationship, it represents a proportionality. Hence, it can never be the answer.

Canberk Özsu
  • 1