When we measure position for example, how does the system "know" that we're measuring position in order to collapse to a position eigenvector? Does the wave function always evolve from the state that it collapsed to? For example, if we measure the position (whatever that means) does the wave evolve from a delta function?
-
"When we measure position for example, how does the system "know"" - are you taking into account the position measurement apparatus? – Alfred Centauri Aug 18 '19 at 11:35
-
3Possible duplicate of How does one make the wavefunction collapse into an eigenstate of a particular operator? – untreated_paramediensis_karnik Aug 18 '19 at 14:11
-
Recent and related post by Sabine Hossenfelder: The Problem with Quantum Measurements – Alfred Centauri Aug 19 '19 at 23:55
-
Jeff, I don't follow. – Alfred Centauri Aug 20 '19 at 02:15
5 Answers
The system doesn't "know" anything.
The only uncontroversial statement one can make about the (strong) measurement of a quantum system is that you will make the correct predictions if you assume that the state after the measurement was the eigenstate corresponding to the measured value of the observable (so, for position, indeed a $\delta$-function, if we ignore issues with that not being a real function, which would be a distraction here). But what we mean by "state" in the first place - i.e. what ontology, if any, corresponds to the statement "the system is in the quantum state $\lvert \psi\rangle$" - is ambiguous to begin with:
Whether the original state "collapsed" to this new state, whether the "state" is just an imperfect representation of our knowledge and the "collapse" is just updating our information (cf. "$\psi$-ontic" vs "$\psi$-epistemic", see e.g. this answer by Emilio Pisanty) instead of an actual physical process, or something else entirely, is a matter of quantum interpretation. In some interpretations, there is collapse, in others there isn't, but in any case, the formalism of quantum mechanics itself does not provide a single "correct" interpretation.
That is, your question is essentially unanswerable unless you specify the interpretation within which it is to be answered. But none of the predictions of quantum mechanics depends on it anyway - you do not need to have a concept of "how" collapse works to compute the outcome of measurements.
- 124,833
-
Interesting I've never heard it explained that way. So the precision of your observation must play a part then, right? If you don't carefully pin something down to exactly one location how could the wave localize to that point? However, I thought that the wave needed to collapse to a basis vector, so which basis does it use? I assume I'm misunderstanding what constitutes a basis vector. Is it more like the wave "constricts" to match the updated possibilities for the state? – Jeff Bass Aug 18 '19 at 03:52
-
3@JeffBass Indeed, a "real" position measurement doesn't project the wave to a point, but rather to something like an interval, but that doesn't change anything fundamental, which is what I meant by the specific example of position and $\delta$-function being a distraction here. The position operator is an annoying example because it has a continuous unbounded spectrum. If you want to know something about the position operator and its measurement specifically, I'd advise you to ask a new question, since your current question reads as if you just use it as a generic operator here. – ACuriousMind Aug 18 '19 at 10:09
-
ACM, your comment above reminded me of reading somewhere, probably in the context of Bohmian Mechanics, that physical measurement of observables other than position nonetheless amount to a position measurement of the particle. – Alfred Centauri Aug 18 '19 at 12:59
-
Ah, here's a recent example from the arXiv: "The reason is that (i) all measurements come down to position measurements and (ii) Bohm’s theory provides a clear and coherent explanation of the measurement outcome statistics based on an ontology of particle positions, a law for their evolution and a probability measure linked with that law." – Alfred Centauri Aug 18 '19 at 13:00
-
I'd change "was the eigenstate" to "was an eigenstate". And not just about constant factors; the eigenspace may be multi-dimensional. – JiK Aug 19 '19 at 10:20
-
I feel like this answer seriously downplays how much we actually can explain wave function collapse. All you need is a density matrix and a description of how the quantum system interacts with the many-degrees-of-freedom measurement apparatus. – DanielSank Aug 19 '19 at 14:22
-
1@DanielSank If you're alluding to decoherence theory, I don't think this "explains" collapse, it just explains why the pointer states of the apparatus always match the state of the measured system, see https://physics.stackexchange.com/a/491972/50583 – ACuriousMind Aug 19 '19 at 17:16
This question is about what is called the "preferred basis problem" and it is a well-studied aspect of quantum measurement theory.
There are two aspects to the measurement problem:
If we adopt the collapse postulate, then for any given measurement-like interaction, how is the measurement basis determined?
What is the nature of the evolution of the system such that it finally arrives in one state of that basis?
The question here is mainly concerned with 1. This is the part of the measurement problem which can be resolved by the study of decoherence, which goes as follows.
It can happen that for one basis an off-diagonal density matrix element such as $\langle \phi_i |\psi\rangle \langle \psi | \phi_j \rangle$ (where $\phi_i$ are states of the basis) will either evolve very quickly or can be sensitive to very small disturbances, whereas for another basis this may not be so. In this case the off-diagonal elements of the density matrix average to zero over any practical timescale, so we have decoherence between states of such a basis. It is called a pointer basis. It is a basis in which the density matrix of the sytem is diagonal. In this case the future evolution of the system is indistinguishable from that of a system which is in one and only one of these basis states, drawn randomly with a probability obtained from the density matrix in the standard way.
One can also get a diagonal density matrix by taking an average over parts of the environment which have become entangled with the system. In either case the resulting decoherence solves the preferred basis problem, but it does not address the wider issue of exactly how to interpret the physical implications of the mathematics of quantum theory. That is, you can still take your pick from single-world or many-world interpretations, and the ontological status of the wavefunction or state-vector is not settled by this type of study.
- 58,183
-
There is no need to "adopt" a postulate. We know what measurement systems do. They exchange energy irreversibly with a quantum system. In case of a position measurement we have to have a piece of matter that can absorb the energy of the quantum at the position of the measurement. The measured coordinates of the "collapse" are simply the coordinates of that piece of matter. One can make a similar argument for all possible measurements. – FlatterMann Oct 10 '22 at 00:40
The collapse happens in all bases. What I mean by that is that the wavefunction can be expressed in any basis you want to. It's just that the easiest basis to look at right after measurement is the one corresponding to what you measured, since the state is the eigenstate corresponding to your measurement.
Always remember the wavefunction isn't physical. It's an abstract thing that we can only describe and "look at" as shadows from their projections. We can choose any projection we want to, but that choice doesn't change the wavefunction.
I guess the essence of my question was how is this "measurement basis" determined? It makes sense that you can still describe the vector in any basis, but my understanding is that measuring the wavefunction in different ways will cause it to collapse differently...so what determines which way it will collapse?
I am not sure what you exactly mean here, but I will attempt to address it. You start with your system in some state $|\psi_\rangle$. You perform a measurement of some observable of your system. Let's say you measure the energy and your (ideal) measurement procedure gives you and energy of $E$. Your system is now in a new state $|\psi'\rangle$. How do the initial and final states relate to each other?
It turns out that the final state is an eigenstate of the Hamiltonian of your system with eigenvalue $E$. In other words $$H|\psi'\rangle=E|\psi'\rangle$$ In other other words, in the "energy basis" your new state only has a non-zero component in one "direction", that being in the "direction" of the basis state whose energy eigenvalue is $E$.
What about the initial state? Well in general is has many non-zero components in the energy basis. i.e (assuming an infinite, discrete energy spectrum) $$|\psi_\rangle=\sum_{n=1}^{\infty}A_n|\psi_n\rangle$$ Where each $|\psi_n\rangle$ is an energy eigenstate. i.e. $H|\psi_n\rangle=E_n|\psi_n\rangle$ where $E_n$ is some energy (of which one is the $E$ mentioned earlier).
So you could describe this "wavefunction collapse" as follows. Before measurement my state was $|\psi\rangle=\sum_{n=1}^{\infty}A_n|\psi_n\rangle$. After measurement my state "collapsed" to one of the $|\psi_n\rangle$ states which we called $|\psi'\rangle$ Is there a way to know which $E_n$ we will get before measurement? No, all we know is the probability of measuring this which is determined by $|A_n|^2$, but we cannot say which state (which "way") this collapse will occur.
However, the point of my answer is that we don't need to work in the energy basis to describe the collapse. We could express $|\psi\rangle$ and $|\psi'\rangle$ in a different basis, say the position basis. Then we would have $$|\psi\rangle=\int_{-\infty}^{\infty}\psi(x)|x\rangle\,\text dx$$ $$|\psi'\rangle=\int_{-\infty}^{\infty}\psi'(x)|x\rangle\,\text dx$$ where $|x\rangle$ are position basis state vectors. The measurement still changed the state independent of the basis we choose ($\psi(x)\neq\psi'(x)$ in general). So the collapse still happened, we can just view it from different bases. For energy, $A_n\to\delta_{n,m}$ where $\delta_{n,m}$ is the Kronecker delta function. For position, $\psi(x)\to\psi'(x)$. But $|\psi\rangle$ and $|\psi'\rangle$ are still the same states in either basis; they are just represented in a different way mathematically.
Therefore, the state vector does not "collapse to a basis". After measurement it can still be expressed in any basis. What you measure determines in which basis it only has one component in though. Perhaps this is what you were wondering. However, we do not know which basis vector in this case, just the probability of ending up with a certain basis vector.
- 56,248
-
1This does not answer the question. The question is not about representing a wavefunction in different bases. – Laplacian Aug 18 '19 at 00:39
-
@eigenvalue I answer the question at the beginning and then qualify and explain my answer. The point is that there isn't a basis that the wavefunction collapses to. You can choose any basis your want. It's just how you represent it. It doesn't go into some basis. – BioPhysicist Aug 18 '19 at 01:53
-
The phrase "since the state is the eigenstate corresponding to your measurement" asserts that the state after the measurement is a basis state of the basis consisting of eigenstates of some given observable (the observable in question being singled out by the nature of the interaction with the measuring apparatus). This seems to me to contradict the rest of your answer. – Andrew Steane Aug 18 '19 at 13:48
-
@AndrewSteane It doesn't contradict anything. Sure, after measurement the state is a basis state corresponding to that operator, but you are still free to express this state in any basis you want to. – BioPhysicist Aug 18 '19 at 13:50
-
@AaronStevens But if the state after a measurement is a basis state, how is it determined which basis the system will use? Is it actually true that the collapse will always go to a basis state? So if I try to measure the position of the particle, even if I don't pin it down all the way, it will collapse to a single mathematical point? – Jeff Bass Aug 18 '19 at 14:55
-
@JeffBass After measurement your system is in a single state given by the state vector $|\psi\rangle$. This is independent of the basis we choose to use. We subjectively choose a basis to express this state in depending on what we want to know about our system. For example, we can use $\langle x|\psi\rangle=\psi(x)$ or $\langle E|\psi\rangle=\psi(E)$ The system doesn't use a basis. It's analogous to how we can express a vector issuing Cartesian basis vectors or polar basis vectors. The system doesn't depend on the basis we choose to use. – BioPhysicist Aug 18 '19 at 15:41
-
@JeffBass Also the wavefunction collapsing to a certain eigenstate doesn't mean it collapses to a point. Remember, these state vectors are not actually physical. Just like how if I'm walking I don't see a velocity vector over my head. – BioPhysicist Aug 18 '19 at 15:43
-
@AaronStevens I see, thank you. It sounds like I completely misunderstood the meaning of "eigenstate". So would it be accurate to say that the wavefunction takes on the state that corresponds to the certainty that we can have about that state? For example if we try to measure its position but don't do a perfect job the wavefunction will become a little "bump"? – Jeff Bass Aug 18 '19 at 16:04
-
@JeffBass That I'm not as sure about. I'm pretty sure the precision of a measurement is different than what you usually see like in the HUP of $\Delta x$ or $\Delta p$. The point I'm trying to make is that after measurement your system is described some state vector, and this vector can be expressed in any basis you want. As ACM suggested, if you have a specific question about a position measurement and what $\psi(x)$ is after it you should post a new question. – BioPhysicist Aug 18 '19 at 17:24
-
There is a real measurement effect in quantum mechanics that is not a matter of philosophical interpretation, and the effect of measurements with respect to different bases is detectably different. I don't see how it is helpful to say that "the collapse happens in all bases" just because of the trivial mathematical fact that you can describe it (or anything else) with respect to any basis. – benrg Aug 19 '19 at 02:14
-
@benrg I'm not saying there isn't a measurement effect. I also didn't say that what you measure doesn't matter. I'm saying that after measurement your system is described by a single state vector. In the "measurement basis" the state has collapsed to a single basis vector (some loose language here), but we can still express this state vector in any basis we want to. The state vector doesn't "collapse to a basis" like the question suggests. The act of measurement doesn't force us to then only use the basis corresponding to the measurement. – BioPhysicist Aug 19 '19 at 03:21
-
@AaronStevens It's been a while since I asked this, but I guess the essence of my question was how is this "measurement basis" determined? It makes sense that you can still describe the vector in any basis, but my understanding is that measuring the wavefunction in different ways will cause it to collapse differently...so what determines which way it will collapse? – Jeff Bass Oct 31 '19 at 16:56
-
-
@AaronStevens Thank you so much for your lengthy response. I hate to keep pestering you, but I think you really hit on it at the end: "What you measure determines in which basis it only has one component in though." To me that just seems so absurd that a physical system would somehow "care" what it is that we're measuring...though I guess that's just the weirdness of QM. I think my question is answered if in practice the system remains slightly fuzzy even after measuring it, but it seems absurd that it would perfectly snap into a particular basis with one nonzero component based on our choice – Jeff Bass Nov 02 '19 at 23:29
-
@JeffBass There are many ways to interpret QM, and I don't claim to be right, but I think that gives the wavefunction much more physical significance than it should. The formalism of QM is very useful and also very odd, but I'm not sure how much of it is "physically influenced". I feel like your comment is analogous to if we looked at classical mechanics and said "Isn't it crazy how this force moves my velocity vector around? Why does my velocity vector care what this force doing?". Vectors are great tools we use, but we don't put that much physical meaning behind them. – BioPhysicist Nov 03 '19 at 01:19
-
But that's just my opinion. It all ultimately just comes down to interpretation. I don't think it's absurd that measuring our system would influence that system, and "wavefunction collapse" is just how we describe that happening. I don't think the system is "aware" of any actual state vector though. – BioPhysicist Nov 03 '19 at 01:20
This "collapse"language is completely navel gazing as far as measurements go.
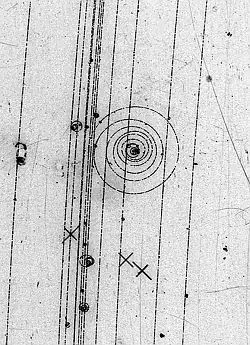
In this answer I show a position measurement, which I copy:
This event was "measured" a few decades ago, by being immortalized in a picture. The data accompanying the picture, the magnetic field ,allow to measure the momentum of the electron, (again and again if one wants) and also the vertex where it appeared. What is collapsing? a balloon? One could remeasure a number of such interactions and derive the probability of a $K^-$ hitting an atom and giving a distribution of the electron momenta. That distribution is connected with the supposedly collapsing wave function!!!
In quantum mechanics , one event means just a sampling from a probability distribution. When you throw dice and get a six, is anything collapsing?
There is one wavefunction describing the $K^-$ riding along towards an electron in an atom, and another wavefunction after the $K^-$ has interacted with an atom . From then on a different wave function will describe the freed electron and the $K^-$ will obey a different wavefunction because its momentum has changed. This means that an accumulation of events will describe these two different wavefunction/probability distributions. Not a single instance.
Thats all.
- 233,453
As far as I know, the "collapse" (or the environmental decoherence that imitates a collapse) is always to the position basis.
I think that a lot of the confusion surrounding this issue comes from the fact that there is a symmetry between position and momentum in the Hamiltonian formalism of QM, so it looks as though wavefunction collapse should have no reason to prefer one over the other. However, in every realistic physical theory, the position-momentum symmetry is explicitly broken by the actual Hamiltonian, which is local in the position basis and not local in any other basis for the position-momentum space. We don't know why this is the case, and we might eventually discover that it is itself the result of some dynamical symmetry-breaking process, but for now the "preferred" status of the position basis is just a brute fact of the laws of physics.
This doesn't mean that the collapse/decoherence is to a Platonic basis of Dirac delta functions. There is presumably something more subtle going on at quantum gravitational scales that we (or at least I) don't yet understand.
- 26,103
-
So... How does this work if we have an atom-cavity system in the superposition of |ground state, photon emitted> and |excited state, no photon emitted>, and we measure an emitted photon? We know that the atom is now in the ground state, which is not a position eigenstate for the electron. – JiK Aug 19 '19 at 10:24