Can the radial oscillations of an elliptical orbit be solved using a fictitious centrifugal potential?

Question

This answer includes the following:

The gravitational potential energy is due to the attractive gravitational force, but for an orbiting object there is also a (fictitious) centrifugal force pushing it outwards. If we calculate the potential energy due to the centrifugal force and add it to the gravitational potential energy we get an effective potential energy:

$$ V_{eff}(r) = -\frac{GMm}{r} + \frac{L^2}{2mr^2} \tag{1} $$

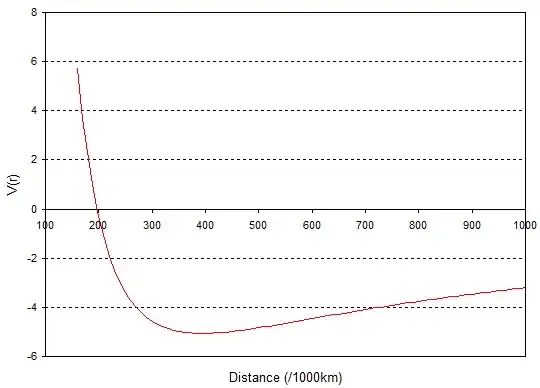
where $L$ is the angular momentum, which is a constant for an orbiting object (because angular momentum is conserved in a central field). If we calculate $V_{eff}$ for an object in a Earth-Moon transfer orbit we get a graph like this:

The stable circular orbit is at the minimum of the potential i.e. at about 384,400km, which is reassuring as this is the Earth-Moon distance. So far so good.

and then goes on include a third term for effects of General Relativity given in the Wikipedia article on Schwarzschild geodesics

Question: I've never seen the mention of a fictitious potential before, or at least not realized it. Does this one result in oscillations in $r$ that match the radial behavior of an elliptical orbit? I'm encouraged by the shape; shallower at larger radius suggesting that the object spends more time at distances larger than average.

Answer 1

Yes. Conservation of angular momentum under the action of a central force allows both the restriction of the orbit to a plane and the elimination of the angular variable in that plane. So central force problems reduce to one-dimensional problems in the radial variable, with an effective potential that includes the “centrifugal” term $L^2/2mr^2$.

With this potential you have reduced the Kepler problem to a one-dimensional problem. The solution for your potential is standard Keplerian elliptical motion.

You can’t get $r(t)$ or $t(r)$ as a simple formula but you can get a nice, complete, analytic parameterized solution $r(E)$, $\theta(E)$, $t(E)$ where the parameter $E$ along the orbit is called the eccentric anomaly. And of course there is a simple elliptical formula for $r(\theta)$.

The mathematical details can be found here.

Answer 2

You can see how to derive the potential starting from the dynamic equations here. However this includes not only the centrifugal force, but also Coriolis an Euler forces when the movement is not circular. And yes, the radial oscillations correspond to the changes in radius during elliptical motion.

Answer 3

How you get the $V_{\text{eff}}(r)$

you get the equations of motion in polar coordinate (Goldstein book) with the Lagrangian

$L_L=T-U$

$$T=\frac{m}{2}\left(\dot{r}^2+r^2\,\dot{\varphi}^2\right)$$

and

$$U=V(r)$$

$\Rightarrow$

$$m\,\ddot{r}-m\,r\,\dot{\varphi}^2=f(r)\quad,f(r)=-\partial_r\,V(r)\tag 1$$

and the first integral

$$m\,r^2\dot{\varphi}=\text{const}=L\tag 2$$

the gravitation potential is: $V(r)=-\frac{G\,M\,m}{r}$ thus:

with (1) and (2)

$$m\,\ddot{r}=-\frac{G\,M\,m}{r^2}+\frac{L^2}{m\,r^3}=f(r)$$

$$V_{\text{eff}}=\int f(r)\,dr=-\frac{G\,M\,m}{r}+\frac{L^2}{2\,m\,r^2}$$

but i didn't use any fictitious force to get the result

Answer 4

You have motion in an effective potential, which included the centrifugal barrier in $1/r^2$. Since this system is conservative, the total energy $E$ is constant and corresponds to a horizontal line on your graph. This line crosses the potential function $V(r)$ at the turning points, so the motion will take place between a minimum and a maximum radius, just like in elliptical motion.

The $1/r$ potential allows for closed orbits in the sense that, as a function of the angle $\theta$ in the orbital plane, $r(\theta+2\pi)=r(\theta)$. Your graph of $V(r)$ cannot show this: you would have to solve the equations of motions for $r$ as a function of $\theta$ to see this. However, there is a classic result known as Bertrand’s theorem which states that closed orbits occur for only specific types of potentials, and the $1/r$ potential is one of them.