Confusion about what happens when the rotating axis of a gyroscope is rotated

Question

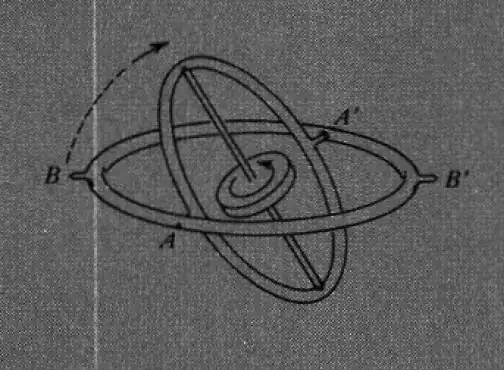
In A.P. French's Newtonian Mechanics, pages $684$ and $685$ , the author said the following about gyroscopes,

If a gyroscope, mounted in its gimbal rings, is set spinning about a horizontal axis, and the outer gimbal is rotated in a horizontal plane, then the inner gimbal ring, carrying the flywheel, tilts up out of the horizontal plane in which it, too, first lay, and after a few oscillations, damped out by friction, the axis of sping of the gyroscope settles down along a vertical direction.

This behavior can be qualitatively understood if one recognizes that the pivots on which the inner gimbal is mounted can supply torques about the vertical direction and about the spin axis of the flywheel, but not about the axis connecting the pivots themselves. This last fact, implying conservation of angular momentum about the axis AA', can be used to explain why the tilting begins. The attempt to rotate the spin axis of the gyroscope in a horizontal plane would, by itself, introduce a component of angular momentum along AA'. The tilting motion provides an equal and opposite angular momentum component that keeps the angular momentum about AA' equal to zero.

The torques that can be supplied via the forces at A and A' are able to perform the main task of canceling out angular momentum about the axis BB' and creating angular momentum about the vertical axis, corresponding to the reorientation of the spin angular momentum $I\boldsymbol{\omega}$ from horizontal to vertical. This process will continue until the axis of the flywheel is fully aligned with the axis of the torque.

I apologize for the length of the excerpt, I tried to give as much context as possible.

Question 1: Where does the torque that rotates the inner gimbal come from if the pivots themselves cannot provide this torque?

Question 2: Which torque exactly is the author referring to in the last paragraph?

Answer 1

The image shows a gimbal mounted gyroscope wheel. From outside to inside there is a yellow frrame and a red frame.

I define three axes:

• Roll axis - the gyroscope wheel spins around the roll axis.
• Pitch axis - motion of the red frame. As you can see, the gimbal mounting ensures the pitch axis is perpendicular to the roll axis.
• Swivel axis - motion of the yellow frame.

Having names for these three axes is necessary. In the excerpt you give the author refers to 'horizontal', and then the reader has to disambiguate as there are two perpendicular horizontal axes. That is why I opt to define 'roll axis', 'pitch axis' and 'swivel axis'

We have that in the setup depicted above the following behavior:
When the wheel is spinning, and you swivel the yellow frame the wheel will pitch. If you swivel gingerly (towards a constant angular velocity), and there is a bit of friction in the bearings of the pitch axis, then the pitching motion will not overshoot.

The author of the book you quoting describes a more violent case. You abruptly start a swiveling angular velocity. Then I do expect the pitching motion to overshoot initially. In the idealized case of absence of any friction the roll axis would keep oscillating. When friction removes energy from the system the oscillating motion will decay to lowest state of energy, which is that the roll axis is aligned with the swivel axis.

So far I have only repeated what you wrote, now to question 1:

When the wheel is spinning, and you swivel the yellow frame, you can think of the wheel as being involved in two rotations, along perpendicular axes: the spinning motion, and the swiveling motion. Now think of the space that is occupied by the wheel in terms of 4 quadrants. (Looking in the direction of the roll axis: left-up, right-up, left-down and right-down) Each part of the wheel is moving successively through those quadrants. In two of the quadrants the section of wheel moving through that quadrant is moving towards the swivel axis, in the other two the section of the wheel moving through the quadrant is moving away from the swivel axis. The responses in each of those quadrants add up to a pitching effect.

(This pitching effect is presented with two additional illustrating images in my 2012 answer to a question titled 'What determines the direction of precession of a gyroscope'

---

The statements by A.P. French about angular momentum are difficult to follow.

Let me try and explain my objection:
Let me take the case of a cannon firing a cannonball. We know why the cannonball shoots out of the barrel: it's because propellent has exploded. The same cause (explosion of the propellent) also causes recoil of the barrel.

The statement by A.P. French about angular momentum is like stating: the cannonball flying out of the barrel is explained by the recoil of the barrel. The problem with that: how you explain the recoil of the barrel? You would have to claim: the recoil of the barrel is explained by the cannonball shooting out. Those two claims together are circular reasoning.

Likewise: Yes, you cannot have violation of conservation of angular momentum, but it's wrong to present that as explanation. Superficially it may look like explanation, but closer inspection will reveal it to be circular reasoning.