3

Gravitational waves can temporarily squeeze the fabric of spacetime itself, and, given enough energy, this could cause a single object in the way to be squeezed with spacetime (that it is in) itself so much, that parts of the single object become separated. Now if this separation is large enough, this could cause the other forces (EM mainly, covalent bonds) that bind parts of the object together to loose contact. Just like when we tear an object apart, the covalent bonds could give in after a while.

enter image description here

Could a powerful gravitational wave cause electrons to emit light?

where John Rennie says:

This may seem a bit odd, but it happens because the gravitational wave changes the separation of objects by changing the geometry of the spacetime around them, not by exerting a force on the objects to move them.

How would a passing gravitational wave look or feel?

where Emil says:

However, for higher GW frequencies, and especially at the mechanical resonance, the system will experience an effective force

Question:

  1. Could a powerful gravitational wave tear apart and object?
Qmechanic
  • 201,751
Árpád Szendrei
  • 28,452
  • One can assume that since the gravitational wave only affects spacetime, even if you "stretched" an object from an apple to the size of a planet, in it's frame of reference nothing would be different. That being said, I'd also like to find out the answer. – twisted manifold Feb 02 '20 at 23:36
  • While it not impossible, it isn't very likely. As this post says, gravitational waves couple very weakly with matter. https://physics.stackexchange.com/q/235574/37364 – mmesser314 Feb 03 '20 at 00:51

3 Answers3

3

Could a powerful gravitational wave tear apart and object?

If the force is strong enough the answer is yes, although the waves we have received until now are many orders of magnitude too small for that. For example, let's take GW150914, which had a received strain of $s=10^{-21} \rm m/m$ and a frequency of $500\rm Hz$, so the sine-function for the wave is

$f=\sin(2\pi \cdot 500 t)$

That gives you a relative acceleration of

$a=s·L·\ddot{f}$

from one end to the other, where $L$ is the length of the stretched object, and $\ddot{f}={\rm d}^2f/{\rm d}t^2$. At LIGO, the length was $L=4000\rm m$, so the maximal acceleration from one end to the other was around $4 \cdot 10^{-11} \rm N/kg$, which is not enough to tear LIGO's arm apart, but if you increase either the strain, the frequency or the arm length, the acceleration and therefore the force would get stronger, and if strong enough even tear apart the object:

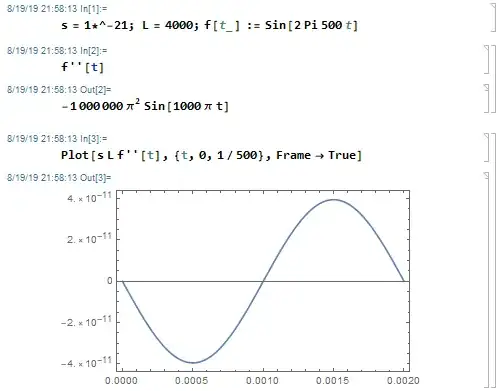
relative acceleration from a gravitational wave

x: time (sec), y: relative acceleration, specific force (m/sec², N/kg)

Either the object is rigid and strong enough to withstand the wave, then its molecules have to accelerate relative to the changing space in order to keep the object from stretching and squeezing, in which case it will feel a force because the electromagnetic forces between the molecules will act against the wave to counteract the deformation.

If the objects are loose and not bound to each other, they will increase and decrease their distance to each other in order to follow their force-free geodesics. If they can not do that because they are bound, they are no longer force-free; in that case it depends if the binding forces between the molecules are stronger or weaker that the required force to cancel out the deformation from the wave.

If you concentrate the masses on the two ends and connect them with a thin string the conversion from acceleration to force and the determination if the string will tear apart is simple, and if you have your mass spread out over the whole distance like on a rigid stick you have to integrate over the distance.

That is also the reason why even objects inside a wave which are not torn apart are at least heated up due to the internal exchange of forces and friction, see Feynman's sticky bead argument. Since the counteraction causes destructive wave interference (if bound objects stay at rest to each other while the space between them oscillates, they oscillate relative to the changing space), the wave is also getting weaker by the amount of energy produced in this process.

Yukterez
  • 11,553
0

The tides that we experience due to spacetime curvature from the Moon and Sun would be stronger for bigger curvatures. We could imagine tides causing breaking of parts of the Earth's crust.

But that effects can be compared to pressure strongly but slowly a glass of crystal, that can break if the force is excessive.

Gravitational waves, even carrying smaller curvatures, would cause vibrations, and ressonance would be an issue, as a specific sound pitch for the glass.

Claudio Saspinski
  • 16,319
  • I think that tides are gravity waves, https://en.wikipedia.org/wiki/Gravity_wave . Any gravitational waves https://en.wikipedia.org/wiki/Gravitational_wave which needs an asymmetry in the mass distributions and acceleration to give curvature change are too weak . – anna v Feb 03 '20 at 05:18
  • @anna v considering that the tide bulge travels across the Earth everyday, for an observer rotating with it, could be called a kind of gravity wave, – Claudio Saspinski Feb 03 '20 at 14:48
  • The tifal wave is called a gravity wave in the sun also and in all the planets and stars. It is not a gravitational wave travelling with the velocity of light. – anna v Feb 03 '20 at 16:13
  • Of course it is not a gravitational wave. If it were, LIGO would have being a waste of money. – Claudio Saspinski Feb 03 '20 at 20:32
0

Yes, there are valid gravitational wave configurations that can result in the separation between two local moving frames, to oscillate between time-like and space-like. I wrote about some of these calculations in here.

But being a valid gravitational wave configuration doesn't actually mean that it is the resulting field of valid gravitational matter source distribution.

lurscher
  • 14,423