Staying in orbit - but doesn't any perturbation start a positive feedback?

Question

I am not a physicist; I am a software engineer. While trying to fall asleep recently, I started thinking about the following.

There are many explanations online of how any object stays in orbit. The explanation boil down to a balance of the object's tangential force with centripetal force.

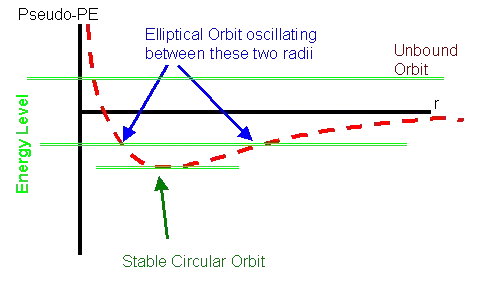
But suppose something upsets this balance by a miniscule amount -- say, a meteorite or a spaceship crashing into Earth. Doesn't this start a positive feedback process to break Earth out of orbit?

Suppose the meteorite crashes such that the Earth is briefly forced toward the sun. (The meteorite contributes to the centripetal force.) Now Earth is just a smidgen closer to the sun. Due to the equation $F=G \frac{m_1 m_2}{d^2}$ that everyone learns in high school physics, the sun's centripetal force acting on Earth in turn increases! That pulls Earth even closer to the sun, increasing centripetal force yet more, and so on.

A similar argument applies to briefly forcing Earth away from the sun.

Empirically, I want to say that there's a buffer, such that if the balance of forces is disrupted by less than X%, we remain in orbit. But I cannot justify any buffer from the equation above.

So, what am I missing? How can objects in orbit suffer minor perturbations in the balance of tangential and centripetal force and yet remain in orbit, when it appears to me that any perturbation starts a positive feedback loop?

Answer 1

An orbit is stable because of conservation of angular momentum.

Suppose we start with an object in an exactly circular orbit and slow it down slightly. That means it is moving at less than orbital velocity so it starts to fall inwards. However as its distance to the Sun decreases the tangential component of its velocity has to increase to conserve angular momentum. So as the object nears the Sun it moves faster and faster, and at its closest approach to the Sun it is moving at well above orbital velocity so it starts to move outwards again. You end up with an elliptical orbit:

(this diagram shamelessly cribbed from Google images)

It's actually very difficult to get something orbiting a star to fall into it, because you have to reduce the tangential velocity to zero. At the distance of the Earth from the Sun the orbital velocity is 108,000 km/h. You would have to slow the Earth by this amount to make it fall into the Sun, and fortunately no meteorite is likely to do that.

On a side note, NASA recently sent the Messenger spaceship to study Mercury, and getting the ship to Mercury was hard because of the need to shed all that orbital velocity. Even though Mercury is a lot closer to the Sun than the Earth is you can't just fall there. Messenger had to use several gravity assists to shed enough speed to allow it to orbit Mercury.

Answer 2

The gravitational potential is what is known as a central force, which means that "how strong" the potential is only depends on how far away you are, and not on what angle you are relative to it.

Having said that, gravitational systems are often treated in terms of an effective potential (full explanation provided on the Wikipedia page) which look like this with distance :

As you can see, there's a dip where it says "circular orbit". That's the most stable orbit, since it requires a fair amount of force to knock it out far enough into an "unbound orbit", where it will not be a nice closed orbit around the sun, but will follow some other open ended orbit (like a parabola for example).

If the Earth was in a circular orbit and it got hit by a small force (like an asteroid), it'll be pushed to one side of that point on the graph, meaning it will move into an elliptical orbit. If the earth is already in an elliptical orbit and it gets hit by a small force, it'll move into a slightly different elliptical orbit. Only if the force is large enough, will it get "knocked out" of orbit.

Even then, it's hard for it to fall into the sun because of conservation of angular momentum. For the earth to loose enough angular momentum to fall into the sun, it will have to dissipate to other bodies somehow, which won't happen if we're hit by only one single asteroid/body. It is conceivable though that if we pass through something like an asteroid belt where we are hit by several thousand of these bodies, we could transfer enough angular momentum away. But that last part is just speculation.

Answer 3

Good question. You are correct in that without any restoring force, an object balanced precariously in an equilibrium position will be unstable. In physics, we use the scalar quantity of "potential" to find the equilibrium positions. These will be the maxima and minima in the potential field. The negative gradient of the potential gives the force.

You've identified the force of gravity, but objects in orbit around a massive body also have angular momentum, which is a conserved quantity, meaning that it doesn't change.

If you write down an effective potential for the Earth in orbit around the Sun that includes a term for the "centrifugal potential", you get

$$ V_{\textrm{eff}}(r) = \frac{L^2}{2mr^2} - \frac{GMm}{r} $$

where $r$ is the distance from the sun, which has mass $M$. The earth has mass $m$ and angular momentum $L = m\omega r^2$. Here, $\omega = v/r$ is the angular velocity of the Earth.

The angular momentum $L$ is a constant value, so this expression is a function of $r$ alone.

Here's what it looks like plotted in functional form:

You see that the Earth resides in a potential minimum and so is against perturbations in the radial direction.

If you take the derivative with respect to $r$ of $V_{\textrm{eff}}(r)$ above, you get back the forces (gravity and centrifugal) in the rotating reference frame.

$$ F = -\frac{d V_{\textrm{eff}}}{dr} = \frac{L^2}{mr^3} - \frac{GMm}{r^2} = - \frac{GMm}{r^2} + m\omega^2r $$

The last term is the centrifugal force. You may remember it as $F_c = mv^2/r$.

Answer 4

Qualitative discussion

(almost math free)

The real key to understand orbits is the conservation of angular momentum. A two body orbit is nice this way insofar as it is a planar system and we get an easy expression for the angular momentum (we'll assume a satellite much, much less massive than the primary and not bother with the canonical transformation into the CoM system).

At any particular point in the orbit, the satellite's velocity will have radial component and azimuthal component. We write $\vec{v} = \left(v_r, v_\phi \right)$. The satellite's angular momentum is $L = m_s r v_\phi$, and this quantity must remain always the same. Since the mass of the satellite is constant we get a relationship between radial distance and azimuthal velocity like $v_\phi = \frac{L}{m_s r} \,$: the closer the satellite gets to the primary, the faster it goes around. (There is also a conservation of energy relationship which lets us understand the radial velocity, but I don't really need that here.)

Now, if you think about the balances of forces you started with you'll see that if the orbiting body has too little velocity for a particular height it will start to drop and pick-up more azimuthal velocity. This doesn't just go on until they forces balance again, but actually overshoots, resulting in the body having too much velocity and starting to rise again causing it to shed velocity, over shoot and end up where it started. And it oscillates in and out around the circular orbit it could have with the same angular momentum.

With all the math you get the elliptical orbits that other answers are talking about.