Hamiltonian of non-regular Lagrangian is well-defined on phase space

Question

In section 1.1.3 of Quantization of Gauge Systems by Henneaux and Teitelboim, it is stated that the Hamiltonian $$H=\dot{q}^np_n-L,\tag{1.8}$$ although trivially a function of $q$ and $\dot{q}$, can also be regarded as a function of $q$ and $p$ since $\dot{q}$ only appears in the combination $$p_n=\frac{\partial L(q,\dot{q})}{\partial \dot{q}^n} \tag{1.5}.$$ They assert this even in the case where one cannot solve for $\dot{q}=\dot{q}(q,p)$. I've been having a lot of trouble understanding this statement. The argument given is that an arbitrary variation of the Hamiltonian can be put into the form $$\delta H=\dot{q}^n\delta p_n+\delta \dot{q}^np_n-\delta{q}^n\frac{\partial L}{\partial q^n}-\delta\dot{q}^n\frac{\partial L}{\partial \dot{q}^n}=\dot{q}^n\delta p_n-\delta q^n\frac{\partial L}{\partial q^n}.\tag{1.9}$$ This however seems a bit hand wavy to me. Can somebody help me to understand this argument better? Does anyone know of a more geometric approach to seeing this? All of the mathematical literature I've consulted thus far on classical mechanics seems to focus on the regular case.

Answer 1

Consider a Lagrangian system with $n$ DOF. In the case where the Hessian matrix $\frac{\partial^2 L}{\partial v^i \partial v^j}$ has constant rank $r$, it is possible to replace $r$ velocities with $r$ momenta in the definition of the Hamiltonian. It is proven in theorem 2 of my Phys.SE answer here, that this Hamiltonian will not depend on the remaining $n-r$ velocities, cf. OP's question.

Answer 2

A way to solve this is to restrict the system to closed paths in a WKB- Approximation. I did read about it in a paper from 1981 or 77 I guess. It was about the Sin-Gordon-Model but I cannot find it atm. Found it: https://projecteuclid.org/download/pdf_1/euclid.rmjm/1250129649. Page 350: "Singular Lagrangian" That might help you .

Answer 3

I just realized of a way to answer this question which has a different flavor from the previous answers. I hope this answer complements them.

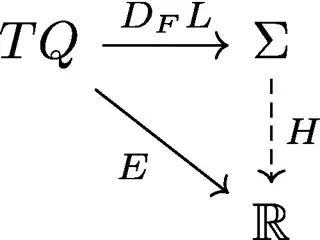
Consider a configuration space $Q$, with coordinates $q$, and its corresponding velocity space $TQ$, with coordinates $(q,\dot{q})$. Given a Lagrangian $L:TQ\rightarrow\mathbb{R}$, we have its fibre-wise derivative $D_FL:TQ\rightarrow T^*Q$. In coodinates, it maps $(q,\dot{q})\mapsto(q,p(q,\dot{q})=\partial L/\partial\dot{q})$. The kind of systems we are interested in are precisely those in which the image of this fibre-wise derivative is a regular submanifold $\Sigma\subseteq T^*Q$.

Now, on $TQ$ we have an energy function $E:TQ\rightarrow\mathbb{R}$, given in coordinates by $$E(q,\dot{q})=\frac{\partial{L}}{\partial\dot{q}^n}(q,\dot{q})\dot{q}^n-L(q,\dot{q}).$$ We may then ask whether there is a corresponding Hamiltonian function $H:\Sigma\rightarrow\mathbb{R}$. In other words, whether such a function exists such that the following diagram commutes.

Of course, this function exists if and only if for any two points in velocity space $(q_1,\dot{q}_1)$ and $(q_2,\dot{q}_2)$, whose image in the constraint surface is the same, have the same energy. Having the same image on the constraint surface means that the velocities are attached to same point $q=q_1=q_2$ in configuration space and the corresponding momenta are equal $p(q,\dot{q}_1)=\frac{\partial L}{\partial\dot{q}}(q,\dot{q}_1)=\frac{\partial L}{\partial\dot{q}}(q,\dot{q}_2)=p(q,\dot{q}_2)$. In particular, consider two such points which are infinitesimally close. From the computation on the question, we have that for arbitrary variations $$\delta E(q,\dot{q})=\dot{q}^n\delta p_n(q,\dot{q})-\frac{\partial L}{\partial q^n}(q,\dot{q})\delta q^n.$$ In particular, for the variation between $(q_1,\dot{q}_1)$ and $(q_2,\dot{q}_2)$, we have $\delta q=\delta p=0$, and thus the energy is invariant. Assuming this result can be integrated for any two points in velocity space, we conclude that indeed our Hamiltonian function exists on the constraint surface.

In coordinates, this means we have our function $H(q,p(q,\dot{q}))$. If we now want to extend this to a function on all of $T^*Q$ (or really on the corresponding coordinate patch), we might as well just consider the function $H(q,p)$ for arbitrary values of $p$ (allowed in the chart).