I have a qualitative understanding of quantum chromodynamics within nucleons and between nucleons, but I do not understand the math behind some of the physics like quark confinement.
What is the math function that dictates the force experienced in quark confinement? What is a simple analogy for this?
So, first off:
The interaction holding a nucleon together (quark to quark) is indeed quantum chromodynamics (QCD). It is mediated by gluons.
The interaction holding a nucleus together ("between nucleons" as you say) is not strictly speaking QCD. It is a residual interaction of QCD, similar to how the Van der Waals force between neutral atoms is a residual interaction of the (fundamental) electromagnetic interaction.
I always find this gif from Wikipedia very pedagogical in differentiating the strong force and the nuclear force (the gluons are the unlabelled balls mediating the interaction among quarks):
As far as I know, there is no analytical proof yet. This is related to the difficulty on performing numerical calculation on QCD due to its strength, making the application of perturbation theory ineffective. Some progress is being done with lattice QCD.
So, you cannot get your proof quantitatively.
However, the main "proof" that colour confinement is "a thing" comes form experiments. Based on these, one can therefore build a qualitative picture.
No one has ever observed a free particles with a colour charge. Be it a gluon, a quark$^\dagger$, or a hadron.
$^\dagger$: The top quark does live on its own for a bit, but it's because it decays before it has time to interact with the strong force and form a bound (colourless) state.
This, in turn, is the reason why the strong force (QCD) is described by an $SU(3)$ and not a $U(3)$ gauge theory. The $U(3)$ one would predict a colour singlet gluon $G_9$ which would have been observed in nature. And it would allow the strong force to be a macroscopic force, which it is not.
As opposed to photons (which mediate the electromagnetic interaction), gluons can self-interact. I mean technically photons also self-interact but only via higher Feynman diagrams so we can neglect that.
Quoting verbatim this book on page 249:
The effect of these [self-]interactions is to squeeze the colour field between the quarks into a tube (a). Rather than the field lines spreading out as in QED (b), they are confined to a tube between the quarks, as indicated in (c). At relatively large distances, the energy density in the tube between the quarks containing the gluon field is constant.
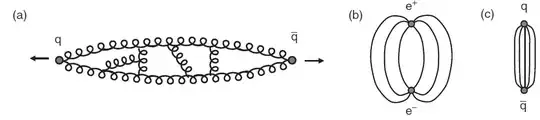
Bottom line, because photons do not self-interact, you cannot "create" field lines out of nowhere which reinforce the EM field between two electric charges. Hence, as you pull them apart, the EM field goes down.
However, for quarks, gluons self-interact and reinforce the field as they are pulled apart. Hence, you can think of the energy density being roughly constant, and hence the potential being of the form: $$ V(\mathbf{r}) \propto \kappa r,$$ where $\kappa$ has been experimentally measured to be about $1$ GeV/fm. In terms of a force, this translates to to $\sim 10^5$ N.
It would therefore take an infinite amount of energy to separate the two quarks. What happens, then, is that the energy stored is converted into $2mc^2$ quarks pairs so as to form colourless bound states, as shown here:
This process is called hadronisation, as it produces bound states of quarks (hadrons).
Nucleons are triplets of quarks ($qqq$), that is baryons, as opposed to mesons that are just pairs. In both cases, they need to be colour neutral. This is achieved either by having as many colours as anti-colours (so mesons are always $q\bar{q}$), or by having all three colours together ($r+g+b = $white). You can also have states with >3 quarks but that's a different story.
The interaction, nuclear force, is a residual of QCD, as discussed at the beginning. Hadrons can therefore only emit and absorb another colour singlet state, i.e. not single gluons (conservation of colour charge). That is why the gif above shows the exchange of pions.
The nuclear potential can be mathematically characterised by a Yukawa potential, i.e. one of the form:
$$V_Y(r) = -\frac{g^2}{4\pi} \frac{\mathrm{e}^{-\frac{mc}{\hbar}r}}{r}, $$ where $m$ is the mass of the mediating particle. In this case, a pion so $m = m_\pi$. The range of the force is $\hbar/(m_\pi c) \sim 1.4$ fm, so quite short-range. Within the nucleus. So "confined" as well.
See also this.
[!doesn't make the image centered; that sequence has no special meaning in SE's Markdown. – David Z Apr 02 '20 at 20:15