0

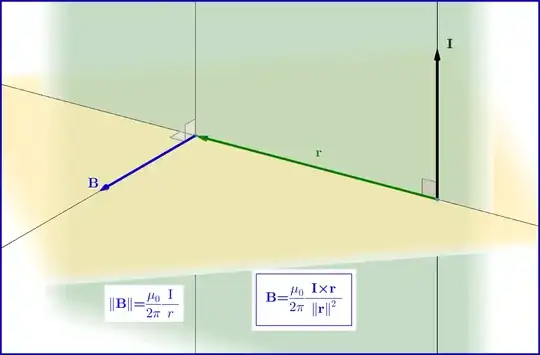
This question is not a homework-exercises, but a request if exist a general formula of Biòt-Savart. We suppose that I have three or more wires traversed by incoming and outgoing currents and I would calculate the resultant of the magnetic field in a generic point of the space.

I have this example where I have a square and in the vertex there are the currents, where $r$ it is the half-diagonal of the square.

enter image description here

EDIT: Added new drawing after the comments of the user @G. Smith because the previous drawing it is not correct the direction and the verse of $\mathbf{B}_{24}$.

enter image description here

If I wanted to find the summation of the magnetic fields due from the 4 (four) wires, hoping that the drawn vectors of the magnetic fields are drawing correctly (if they are not correct or there is a different drawing, I am very happy to know my mistakes), I should to apply to each pair of wires (for example for $\mathbf{B}_{13}$) the relation:

$$\boxed{B_{13}=\frac{\mu_0 (+I_1+I_3)}{2\pi r}}$$ and $$\boxed{B_{24}=\frac{\mu_0 (+I_4-I_2)}{2\pi r}}$$ or $$\boxed{B_{24}=\frac{\mu_0 (-I_4+I_2)}{2\pi r}}$$

Why must I algebraically sum the values of the wire currents? Is there a general formula of Biòt-Savart for this?

Sebastiano
  • 2,529
  • 4
  • 24
  • 45

1 Answers1

1

enter image description here

The magnitude of the magnetic field a distance $\:r\boldsymbol{=}\Vert \mathbf r \Vert\:$ from a long straight wire carrying a steady current I, see Figure, is given by \begin{equation} \mathrm B\boldsymbol{=}\Vert\mathbf B \Vert\boldsymbol{=}\dfrac{\mu_0}{2\pi}\dfrac{\:\:\rm I\:\:}{r} \tag{01}\label{01} \end{equation} while its direction is found by the right-hand rule.

Using the vectors $\:\mathbf I, \mathbf r\:$ and $\:\mathbf B\:$ in place of the scalar quantities $\:\mathrm I, r\:$ and $\:\mathrm B\:$ all these informations are contained in the following simple vector equation \begin{equation} \boxed{\:\:\mathbf B \boldsymbol{=}\dfrac{\mu_0}{2\pi}\dfrac{\:\:\mathbf I \boldsymbol{\times}\mathbf r\:\:}{\Vert \mathbf r\Vert^2}\:\:} \tag{02}\label{02} \end{equation} This is the Biot-Savart Law for a long straight wire carrying a steady current I.

Note : the OP has confused above Law with its use to find the (Lorentz) force per unit length between two parallel wires carrying parallel or anti-parallel steady currents.

Frobenius
  • 15,613