Why does GTR not need a higher dimension to describe the bending of spacetime?

Question

I am a bit confused on how GTR uses intrinsic curvature instead of extrinsic curvature. Maybe it is just a misunderstanding, but I will do my best to describe my question:

If we take an object of $n$ dimensions and want to bend it, we need $n+1$ dimensions. This can be seen if we take a sheet of paper (which we simplyfy to 2 dimensions): If we want to bend it, 3 dimensions are needed!

Similarly, in 3 dimensions, we can only bend a 3-dimensional Cube over 3 dimensions:

So in my understanding, we would need 4 dimensions to bend a 3-dimensional object or spacetime (in this case, a fourth space dimension would be needed in addition to the 3 space and 1 time dimensions of spacetime, so 5 dimensions in total).

However, I've often read that General Relativity does not use a fifth dimension and uses intrinsic curvature instead. How does this compare to the (apparent?) necessity to have $n+1$ dimensions to bend something of $n$ dimensions?

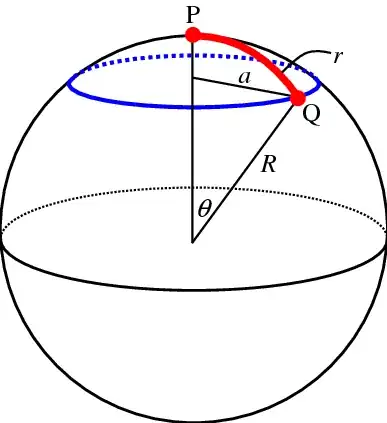
In this answer, the user wrote

Intrinsic and extrinsic curvature are connected in that they both make the same predictions. Just how you do the math is a bit different.

Does this mean that intrinsic/extrinsic curvature is only related to the mathematical process? Or do they also refer to reality?

Even though GTR makes accurate predictions without using any higher dimensions to embed our four-dimensional spacetime, is there any evidence that spacetime must exist in a higher dimension, as this is the only possible way to bend it non-3-dimensional?

_{As I am still in school, I would prefer a non-mathematical answer, but if this is not possible, I will try my best to figure the math out.}

Related Questions:

What is intrinsic curvature? This question focusses on what intrinsic curvature is (as the title says). My question is however more focussed on why intrinsic curvature is possible in the first place.

Answers in Does the shape of the Universe refer to the curvature of spacetime in 5-dimensional space? The answers clarify that it is not necessary to use more than four dimensions, but do not tell how it is possible to bend spacetime if there is no higher dimension.

Update

The answers so far are great and helped me a lot in understanding intrinsic and extrinsic curvature. I still however do not understand why there is no extra dimension needed for intrinsic curvature. According to the answers, extrinsic curvature is not noticed from the brane that is curved (as the bend paper in my first image - the sum of angles is still 180° for every triangle on the plane).

So for intrinsic curvature, we need to bend the paper in a way that it can be measured by hypothetical 2d beings living on the paper, this means the paper must be curved in a way that the sum of angles does not add up to 180°.

This could be achieved by bending the paper in a way that is commonly used in the "bend rubber sheet analogy". This however requires an extra dimension.

So I still cannot understand how in GTR, spacetime can be bend in a way that triangles do not have a sum on angles of 180°, but no extra dimension is needed.

Also, as apparently no extra dimension is needed (which I don't understand), how does this explain the experiment they did with Cassini? (They send a signal from the spacecraft to earth and by taking the time the signal needed to arrive and Cassini's distance, they calculated a path of the signal that was, I believe, 50km than it should have been. Apparently, this was caused by the spacetime curvature of the sun). "Where" was this signal that it moved an extra 50km if there is no extra dimension over which spacetime is curved?

(This last question should not be asked as a seperate question as it is directly linked to my original question)

So, why is there no extra dimension in GTR? I cannot imagine a way of curving spactime in a manner that we can notice it (such as with cassini or the sum of angles) without using an extra dimension.

Update 2

I kind of "accepted" that the analogy of the bend sheet of paper or fabric (which I know is incorrect/incomplete) cannot be transferred to 3d-space or 4d-spacetime and that curvature in mathematics/physics is probably something different that I thought of (with the analogies).

I found the following image:

(Source)

Does this image (I wouldn't call it an analogy anymore) better describe how spacetime is curved/bend/warped? At least, it would explain why there is no 5th dimension.

Extrinsic curvature (specifically the embedding) is arbitrary, so contains no physics. — m4r35n357, Jul 20 '20 at 11:45
@m4r35n357 could you please further elaborate on what this means in regards to my question? And isn't it possible to calculate things using more than 3 space dimensions? — jng224, Jul 20 '20 at 11:47
You can embed a "flat" (2d) plane in 3d by making it into a tightly rolled tube. Tube looks curved, but plane is still flat. Does that help? [EDIT] See @Charles Francis' answer. Incidentally that [EDIT] that I put in seems to give me edit access to the OP. And the second. Didn't touch anything, honest! — m4r35n357, Jul 20 '20 at 14:01
That final image does a pretty good job I think. It may be that the words "curved" and "curvature" are themselves generating part of the confusion. If the words "warped" and "warping" are better at conveying the flavour of the mathematical statements then feel free to use them. — Andrew Steane, Jul 27 '20 at 21:47

Charles Francis · Accepted Answer · 2020-07-21T06:35:29.377

12

First, intrinsic curvature and extrinsic curvature are not the same. When you bend a piece of paper, e.g. into a cylinder, it gains extrinsic curvature, but geometry on the paper is not changed (angles in a triangle, circumference of a circle etc) so it does not gain intrinsic curvature.

It may be possible to mathematically embed spacetime into higher dimensions. At least six dimensions are needed including two time dimensions for even simple cases for which we have solutions, but many more dimensions could be needed for the most general solutions. This would be both conceptually and mathematically difficult (most people think the maths of gtr is hard enough already!), and it is physically unjustified because there aren't any other dimensions into which spacetime can be bent.

Intrinsic curvature is not difficult to understand (at least conceptually), and it needs no concept of bending into higher dimensions. It can be understood in the same way that you see the curvature of the Earth on a flat map, through local scaling distortions of the map. Here is a map of a universe with positive curvature. The central galaxy is not distorted, but greater distortion is seen further from the centre (diagrams from Structures of the Sky more explanation, without maths is given in The Large and the Small)

You can “undo” the scaling distortions on this map by mapping it onto a sphere, showing that the map would be the same whichever galaxy you choose for the centre.

Note that the sphere has no physical meaning. It is just a way of drawing a map. We can also draw maps of expanding spacetime, like this. The galaxies do not get bigger, but the distances between them gets bigger.

Other maps can be used. This one is exactly equivalent, but instead of the universe appearing to expand, galaxies appear to get smaller.

edited Jul 21 '20 at 06:35

answered Jul 20 '20 at 11:57

Charles Francis

11,546
4
22
37

I believe that I now better understand the difference between intrinsic and extrinsic curvature. I have however two new questions: 1. Was it just a misunderstanding of mine to think that GTR uses only 4 dimensions because I thought that extrinsic curvature works without higher dimensions? and 2. In the example with the cylinder, we still need a third dimension for extrinsic curvature; so how does GTR not need a higher dimension? – jng224 Jul 20 '20 at 19:35
Also, as the geometry of the plane is not changed, how would gravity then work? I always thought that this requires the geometry of spacetime to be bend. – jng224 Jul 20 '20 at 19:37
1
this was misunderstanding. Extrinsic curvature needs more dimensions. 2. GTR does not need more dimensions, because everything is described using scaling distortions of maps.

Charles Francis

Jul 20 '20 at 20:02

5

Bending is a really bad analogy. I avoid that word completely! Curvature in general relativity refers to scaling distortions of maps, not to bending in the usual sense. – Charles Francis Jul 20 '20 at 20:03

1

"Extrinsic curvature is not difficult to understand, and it needs no concept of bending into higher dimensions" Are you sure this sentence is correct? – Umaxo Jul 21 '20 at 04:42

@Umaxo, Arrgh a dreaded typo. Thanks. – Charles Francis Jul 21 '20 at 06:37

I agree that for the existence of a three-dimensional curved universe, there is no need for a fourth dimension in which this universe will be bent. But how do you know that "there aren't any other dimensions into which spacetime can be bent"? – Arman Armenpress Mar 13 '21 at 12:50

1

@ArmanArmenpress, it is always possible to introduce parameters, such as other dimensions, which are not inconsistent but which have no impact on physics. Such parameters are "not even wrong". They have no role in science. – Charles Francis Mar 14 '21 at 07:07

Umaxo · Answer 2 · 2020-07-21T05:51:38.177

The questions, which GR wants to answer are all connected to measurements you can do in spacetime. All you can do is measure distances, angles and time passed. If you cannot measure distance through the 4th spatial dimension, then you do not care how exactly is our spacetime embedded in this higher dimensional spacetime. All you need to know, are distances, angles and time passed. All of these are defined strictly in our 4 dimensional spacetime.

Look at this picture:

The bunny is composed from bunch of points and lines connecting neighboring points, which creates triangles. Each triangle tells you what are the distances and angles between neighboring points. In fact, the knowledge of length of every line in the picture is sufficient to answer every question about geometry some 2D physicist living on this bunny could hope to ask (of course in reality there should be infinite amount of infinitely small triangles). And our physicist need not concern himself with 3rd dimension, he only needs to know distances in his 2D space.

The question then is only how to codify this knowledge as best as is possible. Mathematicians came up with two very important machines for that - metric and Riemann curvature tensor, which can be computed from metric.

In your first example, when you are bending sheet of paper, ask yourself what changes does the bend assert on measurements restricted to the sheet itself? If you make it into triangles, the angles remain the same and the distances too. Thus the bend you showed does not actually curve the geometry of the paper at all. You just created extrinsic curvature, but this curvature is inaccessible from the paper. Someone living on the paper thinks it is still as flat as ever.

You could then stretch the paper and this would certainly change the drawn triangles. But this wouldn't still curve the geometry. Stretched paper, is as flat as non stretched one. Triangles changed, but they still obey Euclidean geometry. You can simply view your deformation as simple redrawing of triangles (let us ignore global properties for a while and focus only at small neigborhood of some point of the paper) When you draw a circle, its circumference will be $2\pi r$, where $r$ is radius.

Only once you deform the paper in such a way as to make high school geometry formulas fail will you create intrinsic curvature. Take for example a sphere:

Suddenly, the circumference of the blue circle is not $2\pi r$. It is $2 \pi a$, but the physicist living on the sphere cannot measure this $a$. He thinks $r$ is the radius and thus he will find out that something fishy is going on. The geometry is weird. The space thus must be curved.

@ArmanArmenpress The bunny is 2D, but it is embedded in 3D space and then projected on 2D "sheet of paper" for the picture. — Umaxo, Mar 14 '21 at 08:23
But it is not necessary that this two-dimensional bunny was embedded in a space of a larger dimension, just as it is not necessary that our three-dimensional universe was embedded in a space of greater dimension, is it? — Arman Armenpress, Mar 14 '21 at 08:28
@ArmanArmenpress Depends on the question. In the context of my answer and analogy with GR, it is not necessary, because we are interested only in inner geometry of the bunny. But for student of biology the embedding is necessary in principle, because embedding is not unique in general and biology student might not be able to reconstruct bunny form the knowledge of inner geometry alone. — Umaxo, Mar 14 '21 at 08:56
Thank you for the clarification. That is, it is not at all necessary for our universe to be built into a space of greater dimension. — Arman Armenpress, Mar 14 '21 at 09:07

score 2 · Answer 3 · answered Jul 21 '20 at 06:28

At heart it is simply about the geometry you are using.

In the Euclidean plane the angles of a triangle always add up to 180 deg. But draw a triangle on a sphere and they add up to more. For example a triangle drawn from the North Pole, round the equator for a bit and back to the pole again has two angles of 90 deg each, so the polar angle represents the angular excess.

The key is that you don't need a three-dimensional globe. A flatlander who noticed angles getting bigger the larger the triangle, would develop spherical (or elliptic) geometry anyway. We say that Euclidean geometry is intrinsically flat but that spherical geometry is intrinsically curved.

Analogous distortions in Minkowski spacetime lead us to the realisation that it too must be curved.

Why does GTR not need a higher dimension to describe the bending of spacetime?

3 Answers3

Linked

Related