So, in quantum field theory, how can one describe dynamics of a system of particles? According to what equation does this system evolve? Can one see how this system is moving through space? Is this described by equation of motion for a quantum field or by dynamics of many particle states? In QFT books there is much talk about transitions between many particle states but never have i seen well explained dynamics and how to connect abstract math to a real world motion and dynamics similar to QM.
-
Of course you have seen it, when your QFT books detail the scattering of two particles off each other. Acting on the Fock vacuum with a quantum field you get what? – Cosmas Zachos Aug 11 '20 at 13:30
-
Is this of any help? You may superpose plane waves to get a Gaussian wave packet, but why would you do that? – Cosmas Zachos Aug 11 '20 at 16:13
-
I think you won't get useful answers until you clarify exactly what it is you are asking. A single particle such as an electron is itself quite complicated because it couples to several fields, so several fields are promoted from their ground state when an electron is present. – Andrew Steane Sep 26 '22 at 11:20
3 Answers
QFT (quantum field theory) describes particles as excited states (quanta) of their underlying fields, which are regarded as more fundamental than the particles. Interactions between particles are described by interaction terms in the Lagrangian involving their corresponding fields.
The dynamics is given by the Euler–Lagrange equation applied to the action $S = \int d^4x \mathcal L$, where $\mathcal L = \mathcal L(\phi, \partial_\mu \phi)$ is the Lagrangian density and $\phi$ here for simplification represents all the various fields.
The Euler–Lagrange equation is
$\frac{\partial \mathcal L}{\partial \phi} - \partial_\mu \frac{\partial \mathcal L}{\partial (\partial_\mu \phi)} = 0$
In QFT the fields $\phi$ are promoted to operators and acting on the vacuum state can create or destroy particles. The operator $\phi (x)$ creates a particle at $x$. A realistic description of a particle, i.e. an object localized in a limited region of spacetime, is given via a Gaussian packet. The dynamics of the particles follows from the dynamics of the fields.
- 3,781
-
Yes, all this I know. But still dont see the connection with a wave packet travelling through space.. – Žarko Tomičić Aug 11 '20 at 11:01
-
@Žarko Tomičić, Think of a free field Lagrangian. The equation of motion is the Klein-Gordon which provides plane-wave solutions. – Michele Grosso Aug 11 '20 at 15:09
-
Yes, i read it but my question is much simpler. I actually just want to see logical development with connection to QM. So, quantum fields interact, and in this interaction fields change states, and these states can be called particles. Well, then movement of the particles is actually a behaviour of a field itself. So what is happening with the field to make something like moving particle possible? – Žarko Tomičić Aug 12 '20 at 07:13
-
So, the field is described as phi? Or is phi just acting on the field? – Žarko Tomičić Aug 12 '20 at 07:21
-
1@Žarko Tomičić, The field $\phi(x)$ is regarded as an operator which, acting on the vacuum state, creates a particle state at $x$. If the fields obey to a plane-wave solution, the particles will as well. – Michele Grosso Aug 12 '20 at 07:37
-
@ŽarkoTomičić You have to let go of wave packets. That is not how quantum fields behave. The pretty picture that Anna V shows is not how quantum fields behave. That is the interaction of a high energy particle with matter, which has an entirely different dynamics. How quantum mechanics makes those particle tracks is described in "The wave mechanics of ∝-Ray tracks", Mott (1929). If you want an introduction to how QFT calculates things, start by reading up on path integrals, e.g. Feynman "Space-Time Approach to Non-Relativistic Quantum Mechanics" (1948). Both papers are "gentle". – FlatterMann Sep 26 '22 at 08:16
So, in quantum field theory, how can one describe dynamics of a system of particles?
In general the dynamics are at a $(Δx, Δy ,Δz, Δt)$ region of the four dimensional space , where the interaction described by quantum field theory takes place, the "event", at its center of mass, the system of particles described by Feynman diagrams. When dimensions become macroscopic, there are no interactions to describe, just particle tracks in fourspace.
According to what equation does this system evolve? Can one see how this system is moving through space?
According to classical mechanics.
In this single event picture we see in the recording of a bubble chamber a system of particles coming out of a point as far as our accuracy of measurement goes. The tracks leaving the point are treated with classical mechanics equations. Accumulating such events gives the crossection, calculated using the QFT feynman diagrams.
If one wanted to use QFT to describe the tracks of the leaving particles , not very smart, one would start with wave packets of creation and annihilation operators running across the track.
" but never have i seen well explained dynamics and how to connect abstract math to a real world motion and dynamics similar to QM."
The solutions of the basic QM equations do not describe classical motion of particles in space. Just interaction of particles with potentials.
- 233,453
-
Yes. But lets just say it this way. I can imagine a wave function of a QM particle in space and i know what it means in a way. Main object is wave function and this wave function evolves. Collapse of this wave function happens in certain situations and a particle is now in much narrover region of space. This all can imagine. Now, with qft operators, I dont see this.What is going on? If I have a quantum field of an electron in space-time, what is it? What does it mean? What is now acctually going on? – Žarko Tomičić Aug 12 '20 at 07:05
-
You know, I can imagine dynamics of a wavefunction and hoow this effects what you can call a point particle. I can not imagine dynamics of fields and how do they effect point particle..what is the process.. – Žarko Tomičić Aug 12 '20 at 07:08
-
fields in field theory are like a coordinate system, all over space time at each (x,y,z,t) a plane wave wavefuntion is assumed, no particles. A creation operator on this field creates a particle and an annihilation destroys it, that is the way the particle would progress, except plane waves go from infinity to infinity and the probability of the partice to be at one (x,y,z,t) is infinitessimally small. that is why free particles have to be described with wavepackets, so that they can be localized . http://hyperphysics.phy-astr.gsu.edu/hbase/Waves/wpack.html . That is why I say that to – anna v Aug 12 '20 at 07:14
-
describe the tracks in the picture with wavpackets would not be very smart, since it is mathematically much simpler to use classical mechanics and electromagnetism – anna v Aug 12 '20 at 07:15
-
Arent the creation and anihilation operators just sort of Fourier coefficients that describe the field itself? Same field that can be solved with E-L equations? – Žarko Tomičić Aug 12 '20 at 07:18
-
Not coefficients, they are operators,differentials, , they operate on the fields(i.e.the plane wave wavefunctions) https://en.wikipedia.org/wiki/Creation_and_annihilation_operators – anna v Aug 12 '20 at 09:53
-
They operate on the fields? Arent these operators mathematical representations of the field? Is it not true that electron field is written as a superposition of many creation and anihilation operators? – Žarko Tomičić Aug 12 '20 at 12:08
In QFT all processes are considered to be happening inside the "black boxes", and the theory is aiming at predicting the outputs of the black box from given inputs.
Creation and annihilation operators (and their commutation relations) are used to get rid of input particles and to transform them into ouput particles. We just annihilate inputs and create outputs according to some rules. Black boxes can be visualized as vertices of Feynman diagrams.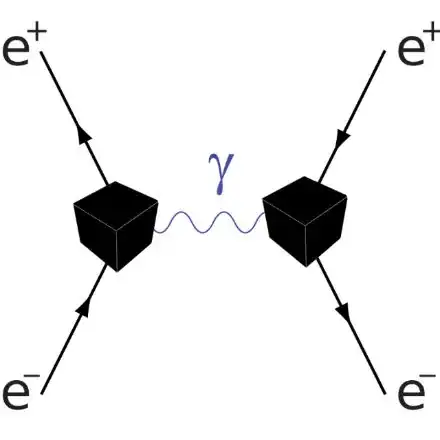
The dynamics study how a physical system might develop or alter over time. In QFT this is achieved by the series of the transformations of inputs to outputs inside the "black boxes".
- 2,305
