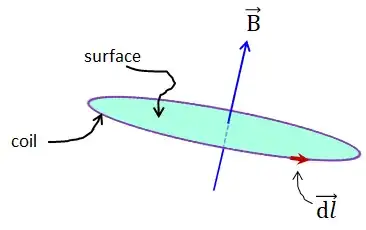
Faraday's law states, $$emf = \oint \mathbf{E} \cdot \mathrm{d}\boldsymbol{l} = - \frac{\mathrm{d}}{\mathrm{d}t} \int \mathbf{B} \cdot \mathrm{d}\mathbf{s}$$
The typical surface we see used to elucidate this law is a single-turn coil of wire like below (purple). Where the surface (green) is a 2-dimensional surface in the plane of the coil that is perfectly normal to the B field everywhere.
My question is about the choice of surface area. I am fairly sure (and @RobJeffries answer here apparently supports) that the surface can take many different shapes as long as it is bounded by the coil. Is my understanding correct?
For example, if i use any of the following surfaces (assuming i can properly handle the integration and dot product on the R.H.S.) i will get the same result for emf as if i used the above surface.
In this case i just "grew" a hollow cylinder up where the coil (dashed black line) defines the open bottom end (the orange surface is not involved in the surface integral on R.H.S.).
In this case below my surface area is the inside of a garbage bag filled with air with the bag opening being perfectly defined by the coil.
In this last case, the surface is the inside of a cone with the open bottom defined by the coil.