Is there a reason behind why Archimedes principle works?

Question

I think most of us are quite aware of Archimedes principle, but is there a reason to why it occurs?

Is it just an observed property? Why is the upthrust equal to the weight of the liquid?

Answer 1

You can understand Archimedes' principle in a simple intuitive way, like Archimedes himself did it. (Search the internet for "archimedes eureka".)

First, the upthrust is independent of the material of the submerged body. Therefore a submarine of iron feels the same upthrust force like a body of water with the same shape.

Therefore, now let's consider a body of water. The body of water doesn't move up or down. So it is obviously in equilibrium. That means the forces (the weight force pointing down, and the upthrust force pointing up) must exactly cancel.

Answer 2

Imagine you submerse a closed container having zero mass in water. If you fill the container entirely with water it should be neutrally buoyant: it shouldn't rise or sink because if you removed the container the water also shouldn't rise or sink. Gravity pulls on the water inside the container with a force $F=\rho_w g V$ where $V$ is the volume and $\rho_w$ the density of the water. This means there has to be upwards buoyant force that cancels this effect. Now you can change the content of the container; you can either suck all the water out leaving a vacuum or replace the water with lead. The buoyant force shouldn't change because it works on the outside of the container and it doesn't know about what's inside. So since $\rho_wV$ is just the weight of the water displaced we see that Archimedes principle is true.

This might feel a bit like a magic trick so let's expand a bit on why this is true. Every point inside a liquid exerts a pressure in every direction. A pressure exerts a force but only over a tiny area. To calculate the force on a submersed object you have calculate the pressure for every point on the surface and them sum all the tiny forces (integrate) to get the total force. In liquids that are static the pressure is given by $p=p_s+\rho g d$ where $p_s$ is the pressure at the surface and $d$ the depth from the surface. The pressure has to increase as you go deeper because each parcel of fluid has to hold up the weight of the column above it. If you draw the pressure for a submersed square you get something like this:

Again, to get the net force you have to sum over all the forces on the surface. Most inward pointing forces cancel but some of the vertically pointing forces don't cancel because the pressure gets larger as you get deeper. You can prove this sum (integral) always gives $\rho_w gV$ but it requires a bit of calculus.

Answer 3

Buoyant force occurs due to the difference in pressure in the liquid.
Consider a cylinder of height h in water

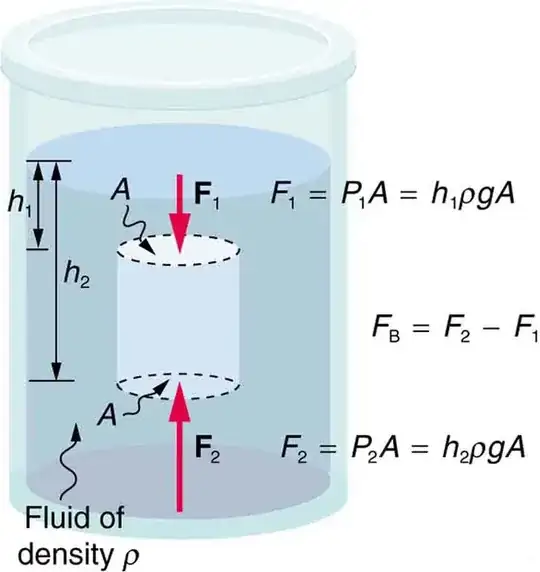
The pressure along its curved side will cancel out because at each height equal pressure is applied from all directions (Pascal's Law).

Therefore only pressure on the flat surfaces contribute to the net force on it

$$F = F_2 - F_1$$ $$F = P_2A - P_1A$$ $$F = (\rho gh_2 - \rho gh_1)A$$ $$F = \rho gA(h_2 - h_1)$$ $$(h_2 - h_1 = h)$$ $$F = \rho gAh$$ $$(V = Ah)$$ $$F = \rho Vg$$ = weight of displaced fluid

Therefore the upward force(buoyant force) on a object in a liquid is equal to the weight of the fluid displaced by it.

Answer 4

If a fully or partially submerged object is removed, the volume of fluid which it displaced will return. Then the distributed pressure forces, which provided the buoyant force on the object, must now support the weight of the returned fluid.