4

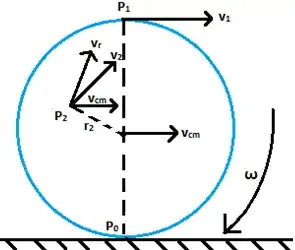
A small doubt in rolling motion. As we know, for pure rolling, the velocity of the lowermost point has to be zero wrt the ground or whatever platform it may be on. Suppose, we have a body (let's say a ring) and it has velocity $v_0$. Assuming the floor has friction, which serves as the torque to cause rolling. I want to find the velocity of the ring after pure rolling has been achieved. My initial thoughts were with the law of conservation of angular momentum on the lowermost point as the net torque about the lowermost point would be zero.

So would the expression be as follows:

$$M v_0 R = M v R + I(\text{centreofmass})\omega$$

or

$$M v_0 R = M v r + I(\text{axis about the lowermost point})\omega$$

My book says it's the former, but I'm a little confused why. In general, for any rotational motion questions if we have to use an axis (not about the one the body is rotating in), would we use the $I$ about its rotational axis or the axis we have taken for the sake of the question. Attaching a pic of a rolling body, in case it helps.

enter image description here

Linkin
  • 2,093
Varun Sudhir
  • 41
  • If you were to use I (centre of mass) that would mean it is moving in circles about the centre, that is, it is slipping. I (about lowermost point) means it is fixed to the ground at that point (as you said velocity of the lowermost point with respect to ground is zero) and it is about that point, the object is rotating, i.e. if the ground were to end right this instant, the object would go about the lowermost point and not the centre. – Rew Feb 02 '21 at 14:06
  • What is $r$ in your notation? – noah Feb 02 '21 at 18:22
  • The radius of the ring. – Varun Sudhir Feb 03 '21 at 01:00
  • What is big $R$ then? – John Alexiou Feb 03 '21 at 13:45

1 Answers1

2

You can use either method, but only your top equation is correct. If you define the rotation axis at the ground, then you must get rid of the $Mvr$ term (or, equivalently, $v=0$ in that term). At any given instant, the motion of the rolling ring is exactly the same as it would be if it were rotating about the instantaneous point of contact with the ground--so it is incorrect to add a translational motion in this case.

Ben51
  • 9,694
  • 1
  • 24
  • 50