1

Hi i am reading about Eddington-Finkelstein coordinates and i read that they do remove the coordinate singularity at $r=r_s$ but still there is some problem with these coordinates which can be removed with Kruskal-Szekeres coordinates. So far i know that in EF coordinates the metric becomes: $$-(1- \frac{2GM}{r})dv^2 + 2dvdr +r^2d\Omega^2$$

I understand that this metric is okay(nonsingular) at $r=r_s$ but could not understand what is the problem with these coordinates. I read that in these coordinates we have increasing time means decreasing radius for $r<r_s$ for ingoing null rays. But i could not understand this statement. My questions are as follows:

  1. What problem do we have with these coordinates?
  2. What does increasing time means decreasing radius for $r<r_s$ ingoing null rays means?
  3. So we have removed the coordinate singularity at $r=r_s$, does this means there is no event horizon for the Schwarzschild black hole?
user12002570
  • 141
  • 1
    "we have removed the singularity at $r=r_s$" - We only moved it from the coordinates to the coordinate transformation. The singularity still exists. It cannot be removed by a valid mathematical transformation that does not involve a division by zero. Moving it out of sight and pretending it no longer exists is widespread, but not rigorous. – safesphere Mar 01 '21 at 15:37
  • I meant "we have removed the coordinate singularity". Check the first line of my question. Thanks for pointing it out though i will correct it in my last question. – user12002570 Mar 02 '21 at 05:08
  • Yes, obviously I was talking about the coordinate singularity. Please read my comment again. A singular transformation removes an asymptotic trend to infinity from coordinates near the horizon, but cannot be applied exactly at the horizon, because it involves a division by zero. You can extend the coordinates through the horizon by manually giving them a desired value at the horizon, but this is a wishful thinking, not physics. As an illustration, what is the value of $(\sin{(1/x)})/x$ at $x=0$? We want it to be zero and can manually set it to zero, but it is not zero. It is undefined. – safesphere Mar 02 '21 at 06:01
  • @safesphere the issue was settled more than 50 years ago. Further reading: https://phys.libretexts.org/Bookshelves/Relativity/Book%3A_General_Relativity_(Crowell)/06%3A_Vacuum_Solutions/6.04%3A_Black_Holes_(Part_1) . – ProfRob Mar 02 '21 at 08:32
  • @ProfRob Total nonsense. – safesphere Mar 02 '21 at 14:53
  • @safesphere Contrarianism in comments, but almost never in answers that could be downvoted, is unhelpful to people seeking conventional answers to conventional questions on this site. That there is a coordinate singularity in Schwarzschild coordinates, that is not a physical singularity, was established more than 50 years ago. i.e. Nothing happens to a freefalling observer at the event horizon of a big black hole. The curvature is finite. – ProfRob Mar 02 '21 at 15:34
  • @ProfRob I am sorry for not living up to the high standards of wishful thinking “established more than 50 years ago”. And I understand your desire to downvote everyone who doesn’t share your misconceptions. Although please note that my comment was a direct quote of you: “Total nonsense” - https://astronomy.stackexchange.com/questions/20340/25497?noredirect=1#comment85202_25497 - Curvature is a tensor with some components diverging at the horizon: https://physics.stackexchange.com/questions/295814 - Your Kretschmann scalar as a norm of the Weyl tensor tells only how the tidal forces scale. – safesphere Mar 02 '21 at 16:40
  • Whatever I wrote that about seems to have disappeared... – ProfRob Mar 02 '21 at 22:42

1 Answers1

2

Here's a picture of Kruskal-Szekeres and Schwarzschild coordinates, with the angular coordinates suppressed. The $X$ and $T$ axes are the Kruskal coordinates, while the curves labeled with values of $r$ and $t$ are the Schwarzschild coordinates. Note that the units are $r_s=1$.

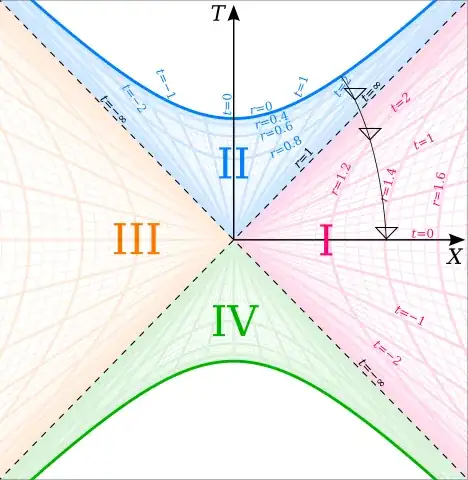
There are two problems with Schwarzschild coordinates. First, they don't cover the regions labeled III (the "second universe" on the other side of the wormhole) or IV (the white hole). This is rarely a problem since those regions don't exist in black holes that form in the normal way from collapsing matter. The second, somewhat more serious problem is that they don't cover the event horizon between regions I and II. In this image, the boundary is labeled $r=1$ ($r=r_s$) and $t=\infty$, but in reality there are no values of $r$ and $t$ that map to points on that dotted line.

Ingoing Eddington-Finkelstein coordinates cover regions I and II and the event horizon between them, which solves the second problem but not the first. There are variants of Schwarzschild and Eddington-Finkelstein coordinates that cover any two adjacent regions, but if you want to cover all four regions at once, you need Kruskal-Szekeres coordinates.

So we have removed the singularity at $r=r_s$, does this means there is no event horizon for the Schwarzschild black hole?

No. There is, objectively, an event horizon. But $r=r_s$ in Schwarzschild coordinates is not the event horizon, it's a coordinate singularity. $r=r_s$ in Eddington-Finkelstein coordinates is the event horizon. (In Kruskal-Szekeres coordinates, the event horizon is $T=X>0$.)

What does increasing time means decreasing radius for $r<rs$ ingoing null rays means?

In region II, there are no null geodesics that hover at a fixed radius or reach larger radii at later times. This is a coordinate-independent fact if you use symmetry properties of the space to define the radius.

benrg
  • 26,103
  • Surely "the event horizon" is independent of the coordinate system we choose to describe events? – ProfRob Mar 02 '21 at 08:34
  • What are the limitations of advanced and retarded Eddington-Finkelstein coordinates? And how does these limitations are resolved by the kruskal coordinates? Also, will $r=r_s$ still be a singularity in kruskal coordinates? Thanks – user12002570 Mar 04 '21 at 06:55
  • @JasonLiam The main limitation of E-F coordinates is they only cover half of the full geometry (which is rarely a problem). $r=r_s$ is only a singularity in Schwarzschild coordinates. I made a few edits to the answer. – benrg Mar 04 '21 at 21:50
  • @ProfRob Yes, the event horizon is objectively a certain surface in the spacetime manifold. There are just no $(t,r,θ,φ)$ Schwarzschild coordinate tuples corresponding to points on that surface. – benrg Mar 04 '21 at 21:54