If we have two conducting charged spheres seperated by some distance, they will interact and assume some form of charge density.
Due to this non trivial charge distribution ,the electric field will be non trivial as well.
How can I find the field then?
Here's a start. While you could use spherical coordinates, that's obviously not ideal. Instead, you can use bispherical coordinates, which use systems of what are called coaxal (not coaxial) circles and their conjugates. So consider this a bit of background.
The radical axis of two circles is the locus of points whose distance to the tangents of the circles is equal. This means if you can draw two tangents, one from each circle, and have them intersect so that the distances to that intersection are equal, you've found a point on the radical axis. In fact, the radical axis is a straight line, and if the two circles are represented by equations $S_1=0$, $S_2=0$, then the radical axis is the linear equation $S_1-S_2=0$.
A system of circles is called coaxal if every pair of circles shares a common radical axis. Meaning there is one radical axis in the system, shared by all circles. These are interesting in their own right, but they're most useful to us for their application to bipolar coordinates. These use conjugate systems of coaxal circles, meaning one system is non-intersecting circles, the other is intersecting circles, and the limiting points of one system are the intersecting points of the other system. We call these points the foci of the system. Taken together, the two conjugate systems of coaxal circles are called Apollonian circles.
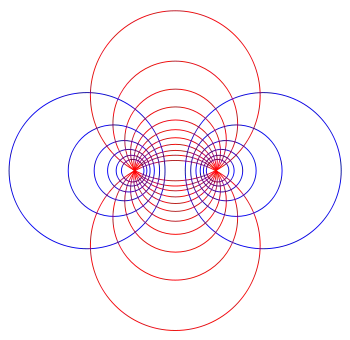
We will need some elementary results about coaxal systems. First, we'll consider the nonintersecting (blue in the image above) species. Fix the radical axis as the $y$-axis, and constrain the circles to all have centers on the $x$-axis. Then they have equations of the form $$ x^2+y^2+2gx+a^2=0 $$ Where $g$ is a parameter which identifies the circle, and $a$, it can be shown, is half the distance between the two foci of the system (the limiting points). That is, the foci are at coordinates $(\pm a, 0)$. As well, the radius of a circle with the form above is $r^2=g^2-a^2$.
The conjugate circles will have equations of the form $$x^2+y^2+2fy-a^2=0$$ Where $f$ is the parameter identifying the circles and $a$ is the same as above. The other results apply.
It can be demonstrated that the circles of one system intersect the circles of the other orthogonally, and thus we can define an orthogonal curvilinear coordinate system based on two parameters, as long as they uniquely identify a point. It turns out, the parameters $g$ and $f$ are not suitable as-is, and so we will define the coordinate system in different parameters: the angle made from lines drawn from a point to the two foci, denoted by $\sigma$, and the natural log of the distances to a point from each of the foci, denoted $\tau$, and given by $$\tau = \log \frac{d_1}{d_2}$$ We will return to these shortly.
Consider the following problem. We are given two circles, $S_1$ and $S_2$, of radii $r_1$ and $r_2$ respectively, separated by a distance (from center to center) of $d$. If these two circles are part of a coaxal system, what is the value of $a$? I.e. what is the separation distance between the foci?
You can solve this for yourself, but I'll provide the answers: $$ a=-r_2^2 + \frac{[d^2-(r_1^2-r_2^2)]^2}{4d^2} $$ We can further find that the second sphere is located at $(-g_2,0)$, where $$g_2 = \frac{d^2-(r_1^2-r_2^2)}{2d}$$ Then the position of the second sphere is $(-g_1,0)$, where $g_1=g_2-d$ (assuming $g_2>g_1$).
In bispherical coordinates, we use $\sigma$ and $\tau$ from above, and the azimuthal angle $\phi$ (same as in spherical). The transformation is: \begin{align} x&=a\frac{\sin \sigma}{\cosh \tau - \cos \sigma} \cos \phi \\ y&=a\frac{\sin \sigma}{\cosh \tau - \cos \sigma} \sin \phi \\ z&=a\frac{\sinh \sigma}{\cosh \tau - \cos \sigma} \end{align} With the inverse transformations \begin{align} \sigma &= \cos^{-1} \left(\frac{R^2-a^2}{Q}\right)\\ \tau &= \sinh^{-1} \left(\frac{2az}{Q}\right)\\ \phi &= \tan^{-1}\left(\frac{y}{x}\right) \end{align} Where $R=\sqrt{x^2+y^2+z^2}$, and $Q=\sqrt{(R^2+a^2)^2-(2az)^2}$.
It's worth noting that, using the complex logarithm, you can rewrite the latter transformations as: $$ \tau+i\sigma = \ln \frac{\rho+i(z+a)}{\rho+i(z-a)} $$ Where $\rho = \sqrt{x^2+y^2}$. To go between the two, you can use the relations $$ \sinh^{-1}(z) = \ln (z+\sqrt{1+z^2}) $$ $$ \cos^{-1}(z) = -i\ln (z+\sqrt{z^2-1}) $$ But it's not trivial to actually go back and forth this way. The $\tau+i\sigma$ form comes from the study of conformal mappings, and that sort of thing comes up a lot in PDEs. See appendix.
We're in curvilinear coordinates, so we would like to know the scale factors. These are \begin{align} h_\sigma &= h_\tau = \frac{a}{\cosh \tau - \cos \sigma} \\ h_\phi &= \frac{a \sin \sigma}{\cosh \tau - \cos \sigma} \end{align} These are used to find differentials in curvilinear coordinates.
Most important for our purposes is the Laplacian, $$ \nabla^2 = \frac{(\cosh \tau - \cos \sigma)^3}{a^2 \sin \sigma} \left[ \frac{\partial}{\partial \sigma} \left(\frac{\sin \sigma}{\cosh \tau - \cos \sigma} \frac{\partial}{\partial \sigma} \right) + \sin \sigma \frac{\partial}{\partial \tau} \left(\frac{1}{\cosh \tau - \cos \sigma} \frac{\partial}{\partial \tau} \right) + \frac{1}{\sin \sigma (\cosh \tau - \cos \sigma)} \frac{\partial^2}{\partial \phi^2} \right] $$
This cumbersome expression is actually here to help us, we're doing a lot of leg work here to make our job later much easier.
Now, a sphere in bispherical coordinates (on the z-axis anyway) is a surface $\tau = \tau_1$, that is, the $\tau$ coordinate surface. The radius of the sphere is used to determine $\tau$, from $$ r_1^2 = \frac{a^2}{\sinh^2 \tau_1}$$ Rearranging gives $$ \tau_1 = \sinh^{-1} \left(\pm \frac{a}{r_1} \right)$$ The position $(0,0,g_1)$ of a sphere is then found from $$ g_1 = -a \cdot \coth \tau$$ Thus we're ready to set up our problem.
Consider two spheres, $S_1$ and $S_2$, of radii $r_1$ and $r_2$ (resp.), separated by a distance $d$. Then, in a bispherical coordinate system formed by revolving a bipolar coordinate plane about the $z$-axis, the first sphere obeys $$ \tau = \tau_1 = \sinh^{-1} \left(\frac{a}{r_1} \right) $$ While the second sphere is $$ \tau = \tau_2 = \sinh^{-1} \left(\frac{-a}{r_2} \right) $$ Where $$ a=-r_2^2 + \frac{[d^2-(r_1^2-r_2^2)]^2}{4d^2} $$ In the space between the spheres, we assume there is no charge present, so that the electric potential $\Phi$ obeys $$ \nabla^2 \Phi = 0 $$ And our boundary conditions can be found in the usual way, assuming the radiation condition, assuming a fixed amount of charge on either sphere, and assuming equilibrium (that the tangential component of $\mathbf{E}$ at the surface of the conductors is zero).
The difficult part here is becoming sufficiently familiar with the bispherical coordinate system that you can quickly set up boundary conditions, then you use separation of variables (which works in this coordinate system) and you can solve Laplace's equation. It may be cumbersome, and it will certainly require a solution in series, but it's not beyond the reach of an undergrad with a course in PDEs. Once you've attempted the problem, you can find the solution in the paper linked in a comment above, Appendix B, or you can check the original paper from Jeffrey which is what the newer paper is based on.
I had some time today, so I thought I would try and solve this to demonstrate. First we write out the equation $\nabla^2 \Phi = 0$, using $\omega(\tau,\sigma) = \cosh \tau - \cos \sigma$:
$$ \nabla^2 \Phi = \frac{\omega^3}{a^2 \sin \sigma} \left[ \frac{\partial}{\partial \sigma} \left(\frac{\sin \sigma}{\omega} \frac{\partial \Phi}{\partial \sigma} \right) + \sin \sigma \frac{\partial}{\partial \tau} \left(\frac{1}{\omega} \frac{\partial \Phi}{\partial \tau} \right) + \frac{1}{\omega \sin \sigma} \frac{\partial^2 \Phi}{\partial \phi^2} \right] = 0 $$ Setting $\Phi(\tau, \sigma, \phi) = A(\tau)B(\sigma)C(\phi)$, and dividing out the common term, this reduces to $$ BC\sin \sigma \frac{\partial}{\partial \tau} \left(\frac{1}{\omega} A' \right) + AC\frac{\partial}{\partial \sigma} \left(\frac{\sin \sigma}{\omega} B' \right) + \frac{AB}{\omega \sin \sigma} C'' = 0 $$ Multiply throughout by $\omega \sin \sigma$, and divide by $ABC$, and we get: $$ \frac{\omega \sin^2 \sigma}{A} \frac{\partial}{\partial \tau} \left(\frac{1}{\omega} A' \right) + \frac{\omega \sin \sigma}{B} \frac{\partial}{\partial \sigma} \left(\frac{\sin \sigma}{\omega} B' \right) + \frac{C''}{C} = 0 $$
Taking the partial derivative with respect to $\phi$ shows that $$ \frac{d}{d\phi} \frac{C''}{C} = 0 $$ Or $\frac{C''}{C} = -m^2$ for constant $m$. Thus we can separate into two equations: $$ \frac{C''}{C} = -m^2 $$ $$ \frac{\omega \sin^2 \sigma}{A} \frac{\partial}{\partial \tau} \left(\frac{1}{\omega} A' \right) + \frac{\omega \sin \sigma}{B} \frac{\partial}{\partial \sigma} \left(\frac{\sin \sigma}{\omega} B' \right) = m^2 $$ The equation for $C$ is easy to solve, just observe that $\phi \in [0,2\pi]$ and $\Phi$ must be periodic in $\phi$ ($\Phi(\phi=0) = \Phi(\phi=2\pi)$) so $$ C(\phi) = c_1 e^{i m \phi} + c_2 e^{-i m \phi} $$ (This is a well-known ODE, so if this isn't familiar, don't worry, you just need more exposure to PDEs.)
The other equation needs to be separated again. We can write it as: $$ \frac{\sin \sigma}{A} \frac{\partial}{\partial \tau}\left(\frac{1}{\omega} A'\right) + \frac{1}{B} \frac{\partial}{\partial \sigma} \left( \frac{\sin \sigma}{\omega} B' \right) - \frac{m^2}{\omega \sin \sigma} = 0 $$
We can't separate until we get the $\omega$ terms out of the partial derivatives (recall $\omega = \omega(\sigma,\tau) = \cosh \tau - \cos \sigma$). Thus, we expand the derivatives: $$ \frac{\partial}{\partial \tau}\left(\frac{A'}{\omega}\right) = \frac{-\sinh \tau}{\omega^2} A' + \frac{1}{\omega} A'' $$ $$ \frac{\partial}{\partial \sigma} \left(\frac{\sin \sigma}{\omega} B'\right) = \frac{-\sin^2\sigma}{\omega^2} B' + \frac{1}{\omega}\frac{d}{d\sigma}\left(\sin \sigma B'\right) $$ And we write out the equation to be separated: $$ \frac{-\sin \sigma \sinh \tau}{\omega^2} \frac{A'}{A} + \frac{\sin \sigma}{\omega} \frac{A''}{A} - \frac{\sin^2 \sigma}{\omega^2} \frac{B'}{B} + \frac{1}{\omega} \frac{d}{d\sigma}\left(\sin \sigma B'\right) - \frac{m^2}{\omega \sin \sigma} = 0 $$ Or, dividing by $\sin \sigma$ and multiplying by $\omega^2$, $$ -\sinh \tau \frac{A'}{A} + \omega \frac{A''}{A} - \sin \sigma \frac{B'}{B} + \frac{\omega}{\sin \sigma} \frac{d}{d\sigma}\left(\sin \sigma B'\right) - \frac{\omega m^2}{\sin^2 \sigma} = 0 $$
Rearranging slightly gives $$ \omega \left[\frac{A''}{A} + \frac{1}{\sin \sigma} \frac{d}{d\sigma}\left(\sin \sigma B'\right) - \frac{m^2}{\sin^2 \sigma}\right] = \sinh \tau \frac{A'}{A}+\sin \sigma \frac{B'}{B} $$
Now what? The equation hasn't properly been separated, so we're stuck. In this situation, we go back to our assumption $\Phi(\tau, \sigma, \phi) = A(\tau)B(\sigma)C(\phi)$ and we consider, how can this be modified to eliminate the $\omega$ term later on? It's not obvious, but some effort will verify that $\Phi(\tau, \sigma, \phi) = \sqrt{\omega} A(\tau)B(\sigma)C(\phi)$ will work. In fact, substituting, and performing the same multiplication as our first attempt: $$ \frac{\sin^2 \sigma \sqrt{\omega}}{A} \frac{\partial}{\partial \tau} \left(\frac{A'}{\sqrt{\omega}} +\frac{A\sinh \tau}{2\omega^{3/2}} \right) + \frac{\sin\sigma \sqrt{\omega}}{B}\frac{\partial}{\partial \sigma} \left(\frac{\sin \sigma B'}{\sqrt{\omega}} + \frac{\sin^2\sigma B}{2\omega^{3/2}}\right) + \frac{C''}{C} = 0 $$ So the $C$ equation separates and gives the same answer for $C(\phi)$ as above, and we expand the remaining terms and simplify. According to this MathWorld page, it should come out to: $$ -\frac{\sin^2 \sigma}{4} + \cos \sigma \sin\sigma \frac{B'}{B} + \sin^2 \sigma \frac{B''}{B} + \sin^2\sigma \frac{A''}{A} = m^2 $$ (But I haven't actually carried out the calculation myself.) Thus $A(\tau)$ can be separated and has the same solution for a second parameter, call it $n^2$, which will be negative: $$A(\tau) = a_1 e^{i n \tau} + a_2 e^{-i n \tau}$$ Finally we have the last equation, for $B(\sigma)$, which might look familiar if you've done separation of variables in e.g. spherical coordinates: $$ B'' + \frac{\cos \sigma}{\sin \sigma} B'+\left[\left(-n^2-\frac{1}{4}\right)-\frac{m^2}{1-\cos^2\sigma}\right]B=0 $$ It's very nearly a Legendre equation! The only issue is the term $\left(-n^2-\frac{1}{4}\right)$, which (by Sturm-Liouville theory) should have the form $l(l+1)$ instead. It should be possible to change $n$ into a constant which gives the form $l(l+1)$, although I'll have to come back and check this later; then the solution for $B(\sigma)$ is simply the associated Legendre functions: $$B(\sigma) = b_1 P^m_l(\sigma) + b_2 Q^m_l(\sigma)$$ And the problem is complete.
The solution is a linear combination of spherical harmonics in $\sigma$, thus while it cannot be plotted (or imagined) in the same way as normal spherical harmonics, the calculations are the same. To find the field $\mathbf{E}$, combine the terms as $\Phi=A(\tau)B(\sigma)C(\phi)\sqrt{\cosh\tau-\cos\sigma}$, using the solutions above (but note that the parameters $n$ and $l$ need to be consolidated somehow first!); this gives the potential $\Phi$; then take the gradient (being sure to take the bispherical gradient) to obtain $\mathbf{E}$ in bispherical coordinates. Finally, if you want, you can transform the components back to Cartesian coordinates.
As a historical note, this problem was one of the first problems in electrostatics to be solved with calculus, first by Biot (1801), and then more thoroughly by Poisson (1813). (Prepare for a plug...) You can read about it on my website here, including translations of the original papers. (Plug over!)
We wish to show that the transformations, $$ \sigma = \cos^{-1} \left(\frac{R^2-a^2}{Q}\right) \quad \tau = \sinh^{-1} \left(\frac{2az}{Q}\right) $$ (where $R=\sqrt{x^2+y^2+z^2}$, and $Q=\sqrt{(R^2+a^2)^2-(2az)^2}$) and $$\tau+i\sigma = \ln \frac{\rho+i(z+a)}{\rho+i(z-a)}$$ (where $\rho = \sqrt{x^2+y^2}$) are equivalent. As mentioned above, to go between the two, you can use the relations $$ \sinh^{-1}(z) = \ln (z+\sqrt{1+z^2}) $$ $$ \cos^{-1}(z) = -i\ln (z+\sqrt{z^2-1}) $$
Plugging these in to $\tau+i\sigma$ gives $$ \ln \left[ \frac{2az}{Q} + \sqrt{\frac{(2az)^2}{Q^2}+1} \right] + \ln \left[ \frac{\rho^2+z^2-a^2}{Q} + \sqrt{\frac{(\rho^2+z^2-a^2)^2}{Q^2} - 1} \right] $$ By adding terms together in the square roots (by multiplying by common factors) we get $$ \sqrt{\frac{(2az)^2}{Q^2}+1} = \sqrt{\frac{(2az)^2+(\rho^2+z^2+a^2)^2-(2az)^2}{Q^2}} = \frac{\rho^2+z^2+a^2}{Q} $$ And similarly, $$ \sqrt{\frac{(\rho^2+z^2-a^2)^2}{Q^2}-1} = i\frac{2\rho a}{Q} $$ (Recall that $Q = \sqrt{(\rho^2+z^2+a^2)^2-(2az)^2}$.)
Now we have $$ \ln\left(\frac{2az+\rho^2+z^2+a^2}{Q}\right)+\ln\left(\frac{\rho^2+z^2-a^2+i(2\rho a)}{Q}\right) $$ We can combine the logs as a product, and expand $Q^2$, \begin{align} \ln&\left(\frac{(2az+\rho^2+z^2+a^2)(\rho^2+z^2-a^2+i(2\rho a))}{Q^2}\right) \\ &= \ln\left(\frac{(2az+\rho^2+z^2+a^2)(\rho^2+z^2-a^2+i(2\rho a))}{(\rho^2+z^2+a^2)^2-(2az)^2}\right) \end{align} This simplifies to $$ \ln \left( \frac{\rho^2+z^2-a^2+i(2a\rho)}{\rho^2+z^2+a^2-2az} \right) $$ (Fun fact, this next part is where I was stuck, I had to ask a MathSE question!) The argument to the logarithm can be rewritten as a difference of squares in the numerator and denominator, which reduces to the desired result: \begin{align} \frac{(\rho+ia)^2-(iz)^2}{\rho^2-(i(z-a))^2} &= \frac{[(\rho+ia)+iz][(\rho+ia)-iz]}{[\rho+i(z-a)][\rho-i(z-a)]} \\ &= \frac{\rho+i(a+z)}{\rho+i(z-a)} \end{align} Thus we can more succinctly write the transformation to bispherical coordinates as $$\tau+i\sigma = \ln \frac{\rho+i(z+a)}{\rho+i(z-a)}.$$
Break down the problem into two regions: outside the sphere and inside the sphere. Inside either sphere, the electric field is zero. This is because charges accumulate on the surface of a conductor, and electric field lines terminate perpendicular to the surface. Outside of the spheres, you can use Poisson's equation: \begin{equation} \nabla^2\phi=\frac{-\rho}{\epsilon} \end{equation} Since the spheres are the only sources of charge, you can reduce Poisson's equation to the LaPlace equation: \begin{equation} \nabla^2\phi=0 \end{equation} The solution is not trivial because you must change to spherical coordinates. Choose your coordinate reference frame such that the spheres are centered on some axis, and your origin is between the spheres. If, for example, you choose to align the centers of your spheres on the X-axis with the origin between them, you would have symmetry along the $Y$ and $Z$ axis when $X=0$. You will also need to choose 2 boundary conditions to obtain your solution.
Or, one could consult the paper "Direct current electric potential field associated with two spherical conductors in a whole-space", by D.F. Aldridge and D.W. Oldenburg, published in 1989 in Geophysical Prospecting, vol. 37, pages 311-330. If I could figure out how to attach a PDF copy of this paper I would, but this is somewhat beyond my capability.
