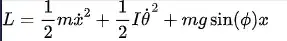1

I was studying the Goldstein Classical Mechanics books and I became confused of this definition here:

Conservation Theorem: If the Generalized Coord $q_j$ is cyclic or ignorable, the corresponding Generalized (or Conjugate) Momentum, pj is conserved.

Well it seems to be a simple definition of a Conservation Theorem by cyclic coordinate. But I was wondering about cases when some coordinates have constrictions.

If a coordinate qj has a holonomic constriction by g(qj)=0, we can say that even if ∂L/∂qj=0, which states that L is not explicit of qj, the generalized momentum is not conserved due to Lagrangian multiplicator terms.

Now the question is, for a coordinate to be cyclic, does it only have to be not explicit about the Lagrangian or does the corresponding Generalized Momentum has to be conserved also?

enter image description here

enter image description here

Which one is correct among the two images?

Here is an example about the constraint problem: enter image description here

enter image description here

enter image description here

If the rolling body has a constraint of no-slip condition (x=Rtheta), friction is applied on the x and theta coordinate. Then we can say the generalized coordinate of x and theta is not conserved. theta is not explicit about L, but can we say theta is cyclic?

Well, as the system has a holonomic constraint(no-slip) the system has no coordinates which the corresponding generalized momentum is conserved. Therefore I was wondering:

enter image description here even if the generalized momentum is not conserved, can the coordinate be cyclic? What if we, suppose change the Lagrangian in a form like: enter image description here It's basically the same Lagrangian except the holonomic constaint is applied. Can we still say the coordinate theta be cyclic?

dc07650
  • 13
  • 1
  • 5
  • I mean, it is a definition, if L does not depend explicitly of X, then X is cyclic. I am not understanding your doubt. The conservation of X momentum comes if, being the lagrangian T-V, the potential not being dependent of $\dot X$, but this is just another thing. – LSS May 11 '21 at 02:26
  • 1
    Please write the question in Mathjax – Physiker May 11 '21 at 07:12

2 Answers2

1

  1. Definition. A coordinate $q^j$ is cyclic if the Lagrangian $L$ doesn't depend on it: $\frac{\partial L}{\partial q^j}=0$.

  2. The corresponding momentum $p_j=\frac{\partial L}{\partial \dot{q}^j}$ is not necessarily conserved unless the Lagrange equations is of the form of the Euler-Lagrange equations, cf. e.g. my Phys.SE answer here.

Qmechanic
  • 201,751
0

Lets make it clear

Case I

you have two degrees of freedom $~x~,\theta$

the Lagrange function is:

$$\mathcal{L}=\frac{m}{2}\,\dot{x}^2+\frac{I}{2}\dot{\theta}^2+m\,g\,\sin(\phi)\,x-(x-r\,\theta)\,\lambda\tag {1}$$

the last term is added because you are not working with generalized coordinate, hence you have to add the rolling condition $~x-r\,\theta~$ and the generalized constraint force $\lambda$

$\Rightarrow~$

$$\frac{\partial\mathcal{L}}{\partial \theta}=r\,\lambda\ne 0$$ $$\frac{\partial\mathcal{L}}{\partial x}=m\,g\,\sin(\phi)-\lambda\ne 0$$

Case II

from the rolling condition you can obtain $~x=r\,\theta~,\Rightarrow\,\dot x=r\,\dot\theta$ so $~\theta$ is now generalized coordinate.

from equation (1)

$$\mathcal{L}=\frac 12\,m{{r\,\dot\theta}}^{2}+\frac 12\,I{\,\dot\theta }^{2}+mg\sin \left( \phi \right) r \theta $$

$\Rightarrow~$

$$\frac{\partial\mathcal{L}}{\partial \theta}=m\,g\,\sin(\phi)\,r\ne 0$$

thus either $x$ nor $\theta$ are cyclic coordinates

Eli
  • 11,878