What is the easiest explanation of a tensor for a non-expert? (not a duplicate question, please read the body!)

Question

I know this question has been asked before, but when I was looking into tensors for the first time I never found a good straightforward explanation of what a tensor is and why it is important. I tried to wrap my head around the topic and express it in the simplest way that requires a minimum amount of math that should be accessible to someone at first year college, and this is what I was able to come up with:

1. Start from vectors: the concept that a tuple [3, 4] represents a point on a coordinate system on a 2D plane should be pretty easy to grasp. This tuple is a vector and can be thought as an arrow starting from the origin and arriving at the point.

2. Typically, one is used to orthonormal systems, so you can introduce a way to calculate the length of the vector thanks to Pythagoras' theorem, that is length = $\sqrt{3^2 + 4^2}$

3. Now realize that [3, 4] just means "three units on the x axis and 4 units on the y axis", so the vector can be written as 3[1, 0] + 4[0, 1]. This introduces the concept of basis vectors, and the fact that every vector on the 2D plane is a linear combination of the basis vectors.

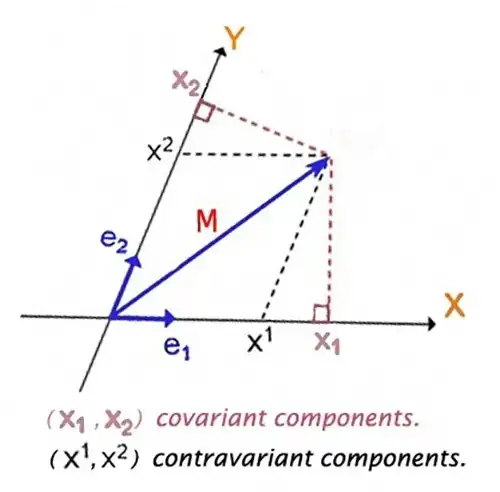
4. Now here comes the question: must the basis vectors be orthogonal and unitary in size? And the answer is no, you can choose a basis with non-unitary vectors and that may be at an angle (as long as the basis vectors are not linearly dependent from each other).

5. The following question is: if you have oblique vectors that are not at right angles, how do you represent vector coordinates? Do you pick ones that result from parallel lines to the tip of the vector, or do you take the ones that result in right angles from the tip of the vector

1. The answer is: both work. This naturally introduces the concept of covariance, contravariance and dual space.
2. And this also introduces a new problem: if the basis vectors are oblique, you cannot use the Pythagorean theorem to calculate the length of the vector, so how do you calculate it? And the answer is that you don't sum the square of the components, but you sum the products of the covariant and contravariant components. That is, from the image above, length of M is $\sqrt{x^1 x_1 + x^2 x_2}$
3. Finally, we get to the tensors. It is clear that an orthonormal basis is just a very special case, where the general case can be an oblique basis with non-unitary vectors. "Regular vector notation" is simply not enough to represent and operate on all the quantities that you need to manage to make calculations on vector spaces. Given a vector, you need to be able to specify both the covariant components and the contravariant components to calculate quantities such as velocity etc. Tensors offer you the possibility to do exactly that: to have an object that can carry information about both covariant AND contravariant components, and it allows you to express concisely quantities like the vector's length etc. Obviously, in an orthonormal basis the covariant and contravariant coordinate coincide, and hence a vector is enough to manage them.

Now, is the above reasoning correct? As much as I have searched in the past for simple explanations like this, I have never found one. Tensors are simply objects that let you represent vectors in any possible basis. They are fundamental when working in various situations, for example in general relativity where spacetime is not a Euclidean space (and basis vectors of different observers are at different angles with each other). The typical description you find: "a tensor is a generalization of a vector: so a tensor of rank 0 is a scalar, a tensor of rank 1 is a vector, 2 is a matrix etc." seems incomplete, or at least it only captures one consequence of tensors (it's like saying that a vector with one component is a scalar, a matrix with one row is a vector, etc., it doesn't tell you anything about these objects). Same for the stress tensor: many use it as an example of what a tensor is, but that's just an application of what a tensor could do, and it does not capture any of the geometrical characteristics I described above.

Given that I'm not an expert in math/physics, my question is really: is the above explanation of a tensor correct / acceptable?

Answer 1

Let's say you've got an $\mathbb R$-vector space $V$ and some function $f:V\rightarrow \mathbb R$ which obeys $$f(a \vec v + b \vec w)=af(\vec v) + b f(\vec w)$$

for all vectors $\vec v,\vec w$ and scalars $a,b$ - that is, it's linear. Congratulations! You've constructed a tensor. The space of such object has a special name - the algebraic dual space of $V$ - and is usually denoted $V^*$ (or something similar). It is also a vector space, which can easily be shown, and elements of $V^*$ are often called covectors.

Now that we have constructed $V^*$, our definition is straightforward: a $(p,q)$-tensor is a linear function which eats $p$ covectors and $q$ vectors and spits out a real number.

A covector can therefore also be understood as a $(0,1)$-tensor. A vector can be understood as a $(1,0)$-tensor, where we define the action of a vector $\vec v$ on a covector $\vec \omega$ as $\vec v(\vec \omega) := \vec \omega(\vec v)$. A linear function which eats two vectors and spits out a real number is a $(0,2)$-tensor. A linear function which eats one vector and one covector and spits out a real number is a $(1,1)$-tensor. So on and so forth.

When we choose a basis $\{\hat e_i\}$ for our vector space, we can talk about components. Say we have a $(0,2)$-tensor $g$. If we feed it two vectors $\vec x$ and $\vec y$ and then expand them in component form as $\vec x = \sum_i x^i \hat e_i$ and $\sum_i \vec y = y^i \hat e_i$, then $$g(\vec x,\vec y) = g\big(\sum_i x^i \hat e_i,\sum_j y^j \hat e_j\big) =\sum_i \sum_j x^i y^j g(\hat e_i,\hat e_j)$$ where we've used the linearity of $g$ to go from the second expression to the third. If we define $g(\hat e_i,\hat e_j)\equiv g_{ij}$ to be the components of $g$ in your chosen basis, then $g(\vec x,\vec y) =\sum_i \sum_j g_{ij} x^i y^j$.

---

Incidentally, note that a $(1,1)$-tensor can also be viewed as a map which eats one vector and spits out another. Why? Well, if $T:V^*\times V \rightarrow \mathbb R$ is a $(1,1)$ tensor, we can feed it a vector $\vec v$ and leave the covector slot open. What kind of object is $T(\bullet,\vec v)$? It's a linear map which eats one covector and spits out a real number - that is, a $(1,0)$-tensor, which is a vector.

This ability to map between different types of tensor by filling some slots and leaving others open is one reason why it's useful to let tensors eat both vectors and covectors.

---

So physically, why are such maps useful? Well, there are plenty of physical examples of quantities which we would expect to be linear functions of vectors.

• The inertia tensor maps the angular velocity of a rotating body to its angular momentum - $\vec L = I(\vec \omega)$ - which means that $I$ is an $(1,1)$-tensor.
• The metric tensor maps two vectors to their inner product - $\vec x \cdot \vec y =g(\vec x,\vec y)$ - which means that $g$ is a $(0,2)$-tensor.
• The Levi-Civita tensor $\epsilon$ which takes three 3D vectors in Euclidean space and spits out the volume of the parallelepiped they define is a $(0,3)$-tensor.

Is the above explanation of a tensor correct / acceptable?

Tensors don't really have anything to do with the orthonormality of your basis. If you're working with a vector space, you will eventually be interested in linear maps on your vector space, which leads you immediately to tensors. I don't really see a more straightforward route than that.

Answer 2

If we're talking about doing physics in $\mathbb{R}^3$, then tensors are the geometric objects that respect the symmetries of $\mathbb{R}^3$, in particular: rotations.

How a tensor behaves under rotations depends on its rank, $n$, and for any rank, there are what are called the natural-form rank-$n$ tensors. A natural-form tensor is both symmetric and traceless in any pair of its indices. That constraint reduces the $n^3$ degrees of freedom down to $2n+1$.

A natural-form tensor's behavior under rotations is irreducible, that is, it can't be broken down into simpler behavior of lower rank tensors. Moreover, the $2n+1$ independent components can be arranged into eigentensors of rotations by $\theta$ about the (arbitrary) $z$-axis, with eigenvalue $e^{im\theta}$ with $m \in (-n,-n+1, \cdots, n)$. The mathematical details of this is covered in the representation theory of Lie groups, $SO(3)$ in the case of $\mathbb{R}^3$.

Their significance to physics is that it seems fundamental physical laws can be expressed as relations between these types of objects.

Rank-0, scalars: A scalar's behavior under rotations is trivial. Nothing happens. They are unchanged. This often leads to statement, "scalars are ordinary numbers", which is misleading. Scalars are geometric objects, numbers aren't. A scalar can be represented by a number, or a field of numbers. But that doesn't make it a number. Regarding a shape, the shape is described by the $l=0$ spherical harmonic (see figure):

$$ Y_l^m(\theta,\phi) = \frac 1 2 \sqrt{\frac 1{\pi}} \propto 1 $$

Rank-1: Vectors. We're all used to ${\bf \hat x}, {\bf \hat y}, {\bf \hat z}$, the three basis vectors in their Cartesian form. To understand them as tensors, it's instructive to consider the spherical basis:

$$ {\bf \hat e}^{\pm}=\frac{\mp 1}{\sqrt 2}({\bf \hat x} \pm i{\bf \hat y}) \rightarrow Y_1^{\pm 1}(\theta, \phi) $$ $$ {\bf \hat e}^0 = {\bf \hat z} = \cos{\theta} \propto Y_1^0(\theta, \phi)$$

The ${\bf \hat e}^{(m)}$ are eigenvectors of $z$-rotations with eigenvalue $e^{im\theta}$.

While it is common, and useful, to think of vectors as arrows with direction and length, that paradigm is difficult to take to higher rank. Instead, think of them as geometric objects shaped like the $Y_1^m$. Either in their real linear combinations:

where they are literally $x$, $y$, and $z$, or in complex form as rotation eigenshapes:

Rank-2 Tensors. A rank-2 cartesian tensor has 9-components: $T_{ij}$ $i, j\in (1,2,3)$, or sometimes $(x,y,z)$. The problem is, there is little intuition to the physical meaning of $T_{xz}$. As part of linear map (well explained in a prior answer)

$$T(\vec u,\vec v)\rightarrow \mathbb{R}$$

it combines $u_x$ and $v_z$with weight $T_{xz}$, but what does that mean physically? It means nothing, because it's coordinate dependent.

To make progress, we need to simplify. The cartesian tensor is reducible, that is, when you rotate it, certain parts don't mix. Step-1 is to define the antisymmetric part:

$$A_{ij} \equiv \frac 1 2 \big(T_{ij}-T_{ji}\big) $$

This tensor has 3 off-diagonal independent terms that can be collected into a axial-vector:

$$ A_i = \frac 1 2 \epsilon_{ijk}T_{jk}$$

which rotates like an ordinary vector (but is even under parity). It's a rank-2 tensor that acts like a vector. Basically, the dyad:

$$ ({\bf \hat x}{\bf \hat y}-{\bf \hat y}{\bf \hat x})/2 \rightarrow {\bf \hat z}$$

rotates like the z unit vector, and so on. Maybe that gives some insight as to what a dyad is, (maybe not?).

Common axial vectors in physics are angular momentum ${\bf \vec L}$, magnetic field ${\bf \vec B}$, torque ${\bf \vec{\tau}}$. Note that a physical law involving axial-vectors on the L.H.S. will not mix them with vectors on the R.H.S., (unless parity is violated). Again, this is the point of tensors, as they are the geometric objects of physical law.

The other part of $T_{ij}$ is the six-DoF symmetric part:

$$ S_{ij} = \frac 1 2 \big(T_{ij}+T_{ji}) $$

From here, we subtract the trace and form the natural-form rank2 tensor:

$$ N_{ij} = S_{ij} -\frac 1 3 {\rm Tr(S)}\delta_{ij}$$

First, note that $\frac 1 3 {\rm Tr(S)}\delta_{ij}$ is a two-index tensor, but it is isotropic. It is spherical, and does not change under rotations. An example of this is the stress tensor of a hydrostatic fluid:

$$ \sigma_{ij}=-p\delta_{ij} $$

While it is a tensor, it transforms like a scalar: the pressure $p$.

The remaining 5 DoF form $N_{ij}$, which obviously satisfies $N_{ij}=N_{ji}$ and ${\rm Tr}(N)=0$. They are geometric objects, and can be put into linear combinations that transform like the five $Y_2^m(\theta, \phi)$:

$$\sqrt{\frac 3 2}N_{zz}\equiv N^{(2,0)}\rightarrow Y_2^0(\theta,\phi) $$ $$\frac 1 2 \big(N_{zx} \pm iN_{yz}\big)\equiv N^{(2,\pm 1)}\rightarrow Y_2^{\pm 1}(\theta,\phi) $$ $$\frac 1 2\big(N_{xx}-N_{yy}- \pm 2iN_{xy}\big)\equiv N^{(2,\pm 2)}\rightarrow Y_2^{\pm 2}(\theta,\phi) $$

and are thus, geometric objects shaped like:

A classic example is the quadrupole moment of a charge distribution:

$$ Q_{ij}=\int{\rho({\bf r}}\big(3r_ir_j-||\vec r||^2\delta_{ij} \big)d^3{\bf r}$$

(In quantum mechanics various tensor operators link orthogonal states with distinct tensor shapes of initial and final states, with overlap given by Clebsch-Gordan coefficients).

Also the moment of inertia:

$$ {\bf I} = \int{\rho({\bf r})\vec r \vec rd^3{\bf r}}$$

The trace part

$$I^{(0,0)} \propto m\langle r^2\rangle$$

is spherically symmetric. The antisymmetric part, $I^{(1,m)}$ is manifestly zero.

The purely rank 2 parts are as follows: $I^{(2,0)}$ describes a prolate or oblate shape. It maintains cylindrical symmetry, but breaks spherical symmetry. $I^{(2,\pm 2)}$ describes the lowest order of "East-West bulging", with the phase defining the longitude, and $I^{(2,\pm 1)}$ is non-zero if there is lopsided (off the principle axes), so it can be diagonalized away. It provides and intuitive and geometric view of the inertia tensor.

Nevertheless, it still retains its meaning as a multilinear map. The kinetic energy (both a scalar and a number in $\mathbb{R}$)is:

$$ T= \frac 1 2 {\bf I}(\bf{\vec{\omega}},\bf{\vec{\omega}}) $$

while angular momentum is:

$${\bf L} = {\bf I}(\ldots,\bf{\vec{\omega}})$$

(note that angular velocity as derived from the reducible part of a cartesian tensor: $\omega_i=\epsilon_{ijk}(r_jv_k)$).

Rank-3. At rank-3, one would think the 27 cartesian components, $T_{ijk}$ are incomprehensible; however, upon reduction into irreducible subspaces, it is much more manageable.

The fully antisymmetric combination of indices is proportional to the isotropic (read: scalar) Levi-Civitta symbol, $\epsilon_{ijk}$. There are three vector combinations, two rank 2 combinations, leaving $2n+1=7$ components of the natural form tensor:

$$N_{ijk}=S_{ijk} - \frac 2{15}(\delta_{ij}S_{llk}+{\rm cyclic\,\,perm})$$

with $S_{ijk}= \frac 1 6T_{\{ijk\}}$ being the symmetric combination of indices.

A physical example of a rank-3 tensor is the quadratic non-linear susceptibility tensor. It is a geometric relation, relating the material polarization vector, ${\bf \vec P}$, to the electric field dyadic tensor, ${\bf \vec E\vec E}$:

$$ P_i=\epsilon_0\chi_{ijk}E_jE_k $$

A similar prescription applies to higher rank tensors that then take on the shapes of the spherical harmonics:

The technique applies to any space on which tensors are defined. For instance, in the question it states that a 1D vector is scalar. It is not. Rather, the vector representation of rotations in $\mathbb{R^1}$ is 1 dimensional, so it transforms like a scalar. Also: The various fundamental fermions and bosons have geometric properties related to the Poincare group.

Meanwhile, back in $\mathbb{R}^3$, if the symmetry group becomes $SU(2)$, the 2-component spinor becomes the fundamental geometric object.

Answer 3

Two defns which turn out to be equivalent:

1. A tensor of rank $p$ is that which acts on $p$ vectors to produce a scalar invariant.

2. A tensor is that which behaves mathematically in the same way as an outer product of vectors or a sum of outer products of vectors.

As you see, no need to mention contravariant, covariant, and no need to mention components or bases. (Please see also comment below which asserts that the definition I have given here is not the most general definition employed in mathematics. However I believe this is the way the term "tensor" is widely employed in physics.)