Why do we treat the whole capacitor as if it would be a single conductor?

Question

I am a high school and I am very confused about redistribution of charges when we connect 2 capacitors, my problems are:

1. why are we treating the whole capacitor as if it would be a single conductor and say that charge will distribute equally in both plates (which doesn't make sense to me) unless the potential/better to say a potential difference of both plates becomes equal so, if that's the case let's take the scenario of what I have shown in the image. why the charge redistribution doesn't occur here? there is a potential difference between both the plates connected, so the charges should flow?

2. why is always the charge redistribution occurs symmetrically on both plates? say the potential of the right plate of below capacitor be "V/2" instead of 0 then the potential difference between both plates connected is different so the charge redistribution should be asymmetrical I,e both plates doesn't necessarily have equal and opposite charges?

3. In my textbook, for series combination it is written that the capacitors must have equal and opposite charges on both plates because if they wouldn't then there will be an electric field inside the conductor connecting both capacitors and that would redistribute the charges until they acquire equal and opposite charge because as the plates as very close the electric field due to positive plate and negative plate are almost equal and opposite at any point inside the conductor, which seems to be logical but there is a problem in it. if we go by this explanation then when two capacitors having equal and opposite charges on both plates are connected then the charge redistribution should never occur because the net electric field inside the conductors connecting the two is 0 always, isn't it?

please help me to understand this at my level, please provide me with a logical explanation for my confusions.

EDIT-since my people are confused with what I am thinking I am adding one more image with what I meant by 0 electric field due to equal and opposite charges on the plates,

Answer 1

From one of your comments I read

In my second statement I am asking why do always the plates of capacitor gets an equal and opposite charge no matter how we connect it in any circuit

Allow me to show that this is in general (and in general I mean not in a circuit) not the case.

The isolated capacitor

The plates of an isolated capacitor can host different amounts of charge, if the net charge of the system is not zero to begin with. Using parallel plate capacitors makes it easy to see that what is equal (and opposite in sign) is the charge on the facing sides of each plate.

This should actually represent portions of infinite facing planes, to the electric field lines should all be vertical

They must have taught you the phenomenon of electrostatic induction. So try to think what happens when - in the distant voids of sidereal space, far from any other conductors - you bring a charged conducting plate with positive net charge Q near another identical, but neutral, plate. Let's say we just materialize it there, at a distance d, like so:

The positive charge on the first plate will attract the negative charge on the nearest face of the neutral plate, leaving the opposite face positively charged. At equilibrium (we need a little bit of time for the electric field to propagate - say d/c - and the charge to rearrange - say a multiple of the relaxation time of the conductor's material), only half of the total charge Q will be present (with opposite sign) on the inner sides of the newly formed capacitor.

If I understand you right, you have a problem in accepting the fact that the 'inner' charges are equal (and opposite). Well, mathematically this results from solving a system of equations that relate voltage and charge in a multi-conductor system. This might be above the level taught in high school (but you can find a lucid description in Pollack and Stump's "Electromagnetism" textbook, if you wish), so let's try to see it in a more intuitive way.

Faraday Lines and Tubes of Flux
Are you familiar with the concept of Faraday's lines? They should be taught in a high school course. Basically, they are a way to represent the electric field orientation and strength in space. Electric field lines emerge from positive charges and sink into negative charges. The more lines are present in a region of space, the stronger is the electric field.

A better way to see this is through the concept of tubes of flux. If you have been introduced to such a concept, then you should know that

1. The charges Q1 and Q2 on the conductor's areas that are at the extremes of a tube of flux are equal in magnitude and opposite in sign.

$$Q1= Q, Q2 = -Q$$

2. The electric flux through an arbitrary cross section of the tube of flux is given by

$$flux = Q/{\epsilon}_0$$

The relevant consequences are summarized in this quote from Branko Popovic's "Introductory Engineering Electromagnetism" textbook (p. 49):

"The entire region in which the electric flux exists can be divided into tubes of equal flux. Each tube can then be represented by a single line of force (say, the line of force along its axis). Since the tube are supposed to be of equal flux, the charges on which they end are also equal. We can represent these charges by a single plus or minus sign. If these conventions are adopted, the magnitude of the electric field intensity is proportional to the density of the lines of force at a point, and the charge density is proportional to the density of the plus and minus signs."

Now, try to imagine the field lines leaving the inner side of the first plate originating from a given fraction of charge there, they will have to end on the the inner side of the second plate on the same amount of charge there. If it can help you, imagine that each charge represented by a single plus or minus sign can only shoot out (if positive) or sink (if negative) one field line, do you see now why you need to have the same amount of charge facing in the interior of the capacitor?
You can't have dangling electric field lines starting from a charge and not ending in another charge. Likewise, the field lines reaching a negative charge cannot come from an empty point in space.

The connected capacitor

Now, when you connect one plate to Earth - i.e. a reservoir of charge that can supply and balance any charge you need without changing its potential, you end up losing the extra charge on the outer sides of the plates and all you are left with is the equal and opposing charges on the inner faces.

The rationale behind this is that the Earth is so big (i.e. it has a humongous self-capacitance) that whatever charge resides on its surface (if you are curios follow this link) ends up so diluted that it appears to have none on the small partial surfaces offered by everyday objects and electronic components connected to it. It just appears that earthing a conducting object drives away any excess charge on it, leaving only the charge that is electrostatically induced by the nearby non-grounded objects.

When we connect a capacitor in a circuit, even if it is not grounded, there is another mechanism that ensures that there won't be excess charge on the outer sides of the plates. Batteries are inherently neutral, so when they offer a charge +Q at the plus terminal, they will have a charge -Q at the minus terminal. If the capacitor you connect is neutral to begin with, you will necessarily reach an equilibrium where positive and negative plates of the capacitor will have identical but opposite charge - charge that once equilibrium is established will end up on the internal facing plates. The plates ends up as being an extension of the battery contacts.

That's why in a circuit context we say that capacitors do NOT store charge, but instead they displace it. In the following I will only consider neutral capacitors, meaning that each capacitor is 'charged' with equal and opposite charges on its facing plates and no residual charge is to be found (in the approximation of negligible fringe effects or of infinite parallel plated capacitor) on the exterior surfaces of the plates.

Multiple connected capacitors

I believe part of your confusion stems from the fact that much depends on how the connection happens: are the capacitors isolated and already charged? Are they connected in a (possibly but not necessarily earthed) circuit and then 'charged'? Let's see what happens in the parallel and series configuration when isolated, pre-charged capacitors are connected and then when the same 'uncharged' configuration is connected to a battery (with a convenient internal resistance to avoid un-physical behavior).

Let's start with two isolated capacitors, each charged independently with charges Q1 for the first one, and Q2>Q1 for the second one. The caps are overall neutral, so the charge will be on the opposing internal faces of the plates. For the intensity of the electric field I am using the number of lines per unit area (the caps are flat and since we neglect fringe effects the field lines are perpendicuar to the plates' surface, ie the flux is the product of the field strenght with the area - if you want to know the voltage, integrate the field or just multiply by the distance, with the correct sign, I do not want to be bothered by these details)

Parallel capacitors
Now, let's see what happens when we connect them in parallel with the same polarity.
The left plate of the first cap, which carried charge +Q1, and the left plate of the second cap, which carried charge +Q2 are now basically a single plate with total charge +(Q1+Q2). The charge cannot go anywhere, and all you have by connecting the plate with a piece of conductor is another conductor. So, in this sense you consider each couple of plates as a single conductor. The charge will in general redistribute in order to give a uniform electric field between the newly formed plates and zero field inside the conductor.

If the caps have the same area, and we do not mess with the distance d between plates, we end up with a two-plates structure with charge Q1+Q2 on a plate of double area on one side, and the opposite charge on the other side. What would the field be in our units of lines per unit area? Correct, the average of the field of the two isolated caps. I have added two more pictures where the area of the capacitors are different (with the same overall amount of total charge Q1+Q2) to show that the field inside is the same, and so is the potential difference across the distance d. That's what you would expect from a parallel connection: both devices are subject to the same voltage which, for identical capacitors, happens to be the average of the voltages of the separated charged caps.

If we connect the isolated caps with reverse polarity, we get a partial cancellation of charge on each plate (the total charge on each newly formed plate would be Q2-Q1 (if we invert the first one wrt to the previous configuration) and the field inside the newly formed cap will be considerably weakened (zero, if the separated charges were identical).

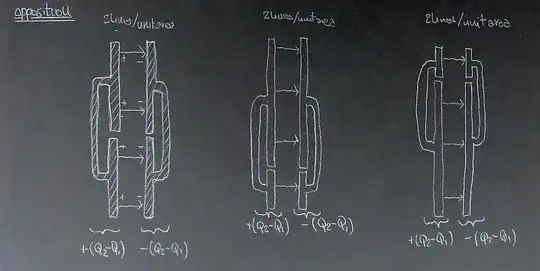
In this case the total field witl be only 2 lines per unit area and the resulting voltage will be half the difference of the voltages of the separated caps.

Now, when you connect the parallel to a battery you won't see anything particularly different because the bottom line of the situation is that of having identical opposite charge on the two plates of the parallel configuration. Of course, now it's the battery that imposes the voltage, so the charge will follow from that. Things can be different though when we consider a series configuration, as your instinct told you (so, here is my +1 to your question)

Series capacitors
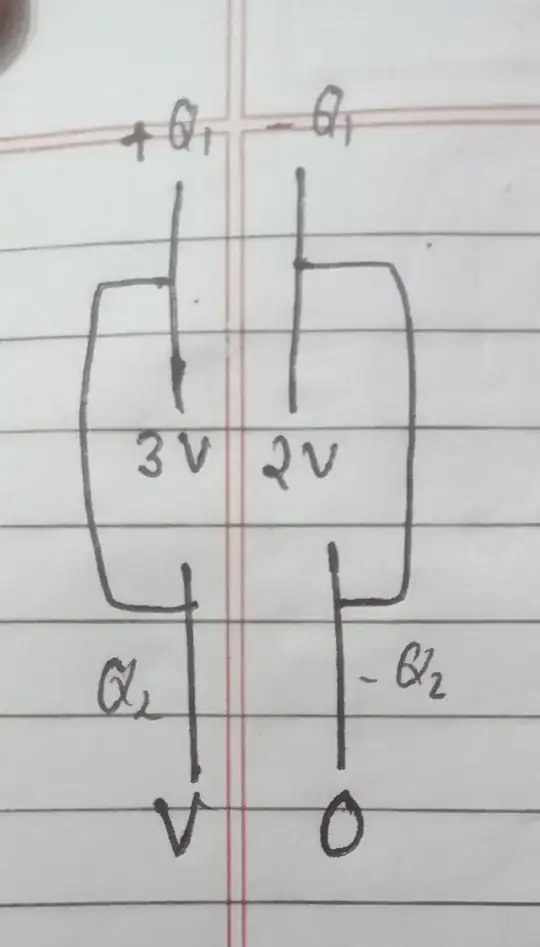
Again, let's start with two isolated charged capacitor, one with charge Q1 (meaning +Q1 on one plate and -Q1 on the other) and the other with charge Q2 > Q1. We bring them together putting one after another, but still as an isolated system.

When we put them in series with the same polarity we get something like this (I added vectors that represent the field generated by the sheets of charge)

Note that we have different charges on the end plates: its Q1 on the leftmost plate and -Q2 on the rightmost plate. It has to be this way because the plates are isolated and they cannot change their charge (this is an ideal system without any leakages). The middle section, composed of two joined plates now is a single piece of conductor with charge Q2-Q1. In the case of Q1=Q2 the net charge on this section would be zero, but charge will still be separated due to the electrostatic induction effect of the charged exterior plates. So, in this case I would say that there is no charge redistribution, but you could see charge separation if you assembled this capacitor by bringing close to each other the two outermost charged plates and the neutral middle section. Whether or not charge will be distributed will depend on how you assemble the final configuration.

Now, something different happens when we have a series capacitor connected to a battery. In this case the charge on the outermost plates is imposed by the battery connection and we can no longer have different charges on the outer plates. We start from +Q on the leftmost plate and -Q on the rightmost one, and the inner section responds by polarizing itself via electrostatic induction.

fig series of two caps - connected to battery

At equilibrium, the neutral section will see its charge displaced so that -Q faces the +Q on the left, while a charge +Q faces the -Q charge on the right. This will also happen with any series of capacitors: the charge is the same (sign apart) on all the plates: what changes when the capacity is different, is the electric field between plates, hence the voltage drop across each capacitor.

One more thing:
What happens in the isolated case when we place the series capacitors in opposition? If we place the caps in series with opposite polarity, we will have a new structure with +Q1 on the first plate, -Q1+Q2 on the central section, and +Q2 on the rightmost plate. If Q2>Q1, we have a central section that has a negative overall charge, while both exterior plates carry a positive charge. The system is overall neutral, as were the two separated capacitors before connection, but the new isolated structure will show a field like this

fig isolated series of two caps - opposite polarity

As you can see, the final result depends on how the constituent parts are put together, and on the connections - or more generally, interactions - with the rest of the world.
If we bring a non-neutral isolated capacitor (or even a neutral real capacitor with fringe effects) near a bigger conducting body connected to the Earth - something we could call a ground plane - even if we do not connect any part of it to the body, electrostatic induction will displace charges in the bigger body producing a different configuration in the distribution of charge and the values of the potentials.

When you have several conductors, it is best to approach the problem by writing a system of equations in the coefficients of potential or in the coefficients of electrostatic induction (or, as some call them, coefficients of capacity). Trying to solve such problems with intuition could easily lead to the wrong solution (and this post is no exception!).

Answer 2

Excellent questions for a student at your level. Here's an attempt at answering them.

1. The situation you've drawn can't occur. The potential difference is determined by the electric field, which in turn is determined by the charge distribution. In the absence of external charges, you're not free to set the potential any way you want, and then also set the charge distribution independently. In addition, if $Q_1 \neq Q_2$, then you have a net charge on each disconnected component of your circuit, so you'd expect that in the steady state there would be a net potential difference between these two components.

2. I'm not sure I understand this question. "the potential difference between both plates connected is different"; the potential difference between which plates and which plates? From your wording, it sounds like you're associating a potential difference to each plate, but a potential difference, as the name suggests, is a property defined between two points.

3. I assume you mean when you connect the two capacitor plates with a wire going around the outside of the capacitor. In that case, we're no longer at a steady state: the wire is able to propagate an electric field from one plate to the other. There will be a field inside the conducting plates.

Answer 3

Answer to Question 3

Question 3: If two caps, each one's plates possessing equal and opposite charge, are connected in series, then this supposed redistribution of charges should never occur. This follows from the last point above, doesn't it?

First and foremost is the answer to the third question. Your understanding that unbalanced charges within the capacitors lead to an electric field in the connecting conductor, causing charges to flow till balancing occurs - is correct and in line with your textbook's.

The source of your confusion is that you have taken the explanation provided in the book about what would have happened if the charges within had been unbalanced and concluded that this is what always happens. Not at all. If you connect capacitors whose charges are already balanced within they, will stay so. The books argues in the manner of a counterfactual.

In fact, it is impossible to get an ideal capacitor charged in such a way that its plates have different charges. That violates charge conservation as the total charge before, during and at the end of charging must remain same. If a cap is uncharged initially, it stays uncharged on the whole.$^1$ (Also see answer to Question 2.2 below)

Answer to question 1.1

Question 1.1 Why do we treat a whole capacitor as if it is a single conductor and say that charge will distribute equally on both plates? This doesn't makes sense to me.

The fact that charge redistributes equally on both plates of a parallel plate cap. doen't imply that we are treating the whole cap. as a single conductor. What makes you think that? The charges (be careful here, counterfactual alert) if were different on the two plates won't need the cap. to be a single conductor to redistribute. They would instead utilise the external circuit in which they are connected to physically redistribute themselves.

Answer to question 1.2

Question 1.2 Unless the potential, or should I say potential difference, of both plates becomes equal. Does it?

It isn't clear what you are trying to say here. First of all it would be either "potential of both plates"(relative to what?) or "potential difference between the plates" but not both in same sentence. Refrain from such careless language.

Are you trying to say that charges will redistribute till the potential of the two plates of a cap becomes (their potential difference becomes $0$)? If so, that is not the case. After balancing of charges within a cap., it has a potential given by its defining property $CV$

Answer to Question 2.1

Question 2.1 Why doesn't charge redistribution occur here? There is a potential difference between both the plates connected, so the charges should flow, shouldn't they?

The labeling of your circuit diagram without any explanation is hard to interpret. Is there some external field keeping the plates at the potentials they are at? Even so how are to two conductors connected by a wire but aren't equipotential?

Refering to your comment (even though you say its regarding your first statement)

In my 1st statement , I am asking that say that we have charged any capacitor with a battery of potential difference say potential at its positive terminal is 3V(reference w.r.t infinite) and potential at negative terminal is 2V and after charging we disconnect it and say we charge an another identical capacitor with a battery of potential difference V (say V at its positive terminal and 0 at its negative terminal) then we disconnect it and connect it with the capacitor we have charged before, then will the charge redistribution will occur or not? if not why not?

I think you simply meant two caps both charged to potential V. There shall be no charge flow in this case. (By using explicit potential values without any explanation, you made it quite difficult understand your question.)

Keep in mind that after disconnecting the caps from their charger batteries, their ends have no memory of what the absolute potentials were wrt. infinity. All that matters is the difference be $V$. This is because potential everywhere is only defined upto addition of a constant. And so

There is a potential difference between both the plates connected...

isn't true as there is no potential difference between the plates on the left (or right).

Answer to Question 2.2

Question 2.2: Why does the charge redistribution occur symmetrically on both the plates of a capacitor in the circuit above? Say the potential of the plate with potential $0$ be changed to $V/2$. Now the potential difference between the bottom capacitor's plates is different than the top one's, so why is the charge redistribution not asymmetric within each cap i.e. why are each cap's plates still exhibiting equal and opposite charge?

I take it you meant

In my second statement I am asking why do always the plates of capacitor gets an equal and opposite charge no matter how we connect it in any circuit and also when we connect it with another capacitor like I have shown above? I am saying that if the potential of the plate was" v/2" instead of 0( reference is w.r.t infinite) and we then connect it like I have shown above then the potential difference between positive plates of both capacitor is not same as the potential difference between negative plates of both capacitors connected then why still the charge redistribution occurs symmetrically?

First of all, since one cap. is charged to $V$ while the other to $V/2$ charge redistribution will occur as there is now relative potential difference between the plates on the left (or right). While you may understand why the capacitors still stay neutral on the whole by using the answer above to question 3, there is another way to look at it. There is charging/discharging current created during charge redistribution. This current is same throughout the circuit. This current deposits a charge $Idt$ on one plate of the capacitor and extracts the same from the other. Thus both increasing the charge while keeping net charge zero. The reverse happens at the other cap. In this way though chrges are moving across the caps. within each net neutrality is maintained.

---

$^1$ Note that this argument doesn't depend on the geometry of the capacitor. Though you mayn't realize this know, the electrical properties of a capacitor that you study may study like its $IV$ relation, its energy content, its $AC$ response, its behaviour in circuits - its all independent of the geometry of the circuit.

Answer 4

This configuration is an example of a more general case of the behaviour of a material under an electric field.

If between the plate of the left side of C1 and the plate of the right side of C2 in the fig 2.26, there was an isolant, the result would be an electric field in the region.

Because it is a conductor, any electric field results in a displacement of charges. So the electric field in the region is zero.

This effect is produced by the displaced charges. For E be zero in the region, the charges of the right plate of C1 and left plate of C2 must be such to generate an E-field that exactly opposes the original. So, the charges are respectively -Q and Q.

Answer 5

The charge equalization does occur in your first picture. You've drawn an unbalanced situation that can't exist at steady-state (i.e. equilibrium).

The charges between the plates will redistribute so that the net electric field between the plates is zero. This occurs even when the voltage supply is 0V. As long as there is a net electric field between the plates, the forces are unbalanced and will work to redistribute the charges until the electric field is zero. It doesn't matter whether this field is being produced by the charges themselves or by the voltage supply.

So even if the voltage supply was 0V, if you had an initial charge distribution producing 3V and 2V on the plates, the charges (either positive or negative depend on which you want to look at) would still redistribute because the charges themselves are producing a net electric field between the plates that repels them away from each other. They'll keep repelling until an equal number of charges ends up on both plates so that the net electric field is zero at which points there is no more net force and the charges stop moving.

If the voltage supply is not 0V, everything still behaves the same except now there is also a second electric field being applied across the plates by the voltage source which also acts on the charges. The charges still have to redistribute until the net electric field between the plates is zero, because as long as it is non-zero there is a force acting to move the charges. It doesn't matter whether this field is externally applied or whether it is from the unbalanced charges themselves.

When the supply was 0V the only fields being produced anywhere in the circuit were from the charges themselves, so in order to produce a net electric field of zero between the plates the charges just had to cancel their own fields out which means an equal number of charges on both plates. When the voltage supply is non-zero, a second electric field is introduced in the circuit and produces an "offset" or asymmetry. So in order to cancel out the electric field between the plates, the number of charges now has to be different on each plate in order to compensate for the voltage supply's electric field.

Answer 6

Q1

To begin, we are not treating "the whole capacitor as if it would be a single conductor". A capacitor consists of two separate conductors (plates) separated by an insulating medium.

The upper and lower capacitors are connected in parallel. Therefore the voltage across each capacitor has to be the same (3-2=1v), not different as you have shown, and the potential on the plates connected by the wires must also be the same.

If you assign a potential of zero on the lower right plate (which is theoretically a purely arbitrary decision) the potential of the upper right plate also has to be zero and the potential everywhere else is measured with respect to the assigned point of zero potential. Then the voltage on the left plate of each capacitor would have to be 1 volt for a potential difference of 1 volt.

Since the charge is different on the pairs of plates, their capacitances also have to be different because

$$C=\frac{Q}{V}$$

Then, if $C_1$ and $C_2$ are the capacitances of the upper and lower pairs of plates, respectively,

$$C_{1}=\frac{Q_1}{V}$$ $$C_{2}=\frac{Q_2}{V}$$

Where, in this case, $V$ = 1 volt.

The charge will not redistribute because there is no potential difference between the plates connected by the wires and the electric field of each capacitor will hold the charge in place.

Q2

why is always the charge redistribution occurs symmetrically on both the plates?

To understand why the charge has to be symmetric on both plates of a capacitor you need to understand how a capacitor gets "charged" in the first place. Consider the charging of a capacitor by a battery in series with a resistor (to limit the current).

Assume the capacitor is not initially charged. Then before it is connected to the battery each metal plate has an equal amount of protons (positive charge) and highly mobile electrons (negative charge) so that each plate is electrically neutral and there is no voltage (potential difference) between the plates.

When the capacitor is connected to a battery, the positive terminal of the battery attracts electrons off of the plate connected to it moving them to the positive terminal of the battery. This leaves a deficit of electrons on that plate making it positively charged.

Simultaneously, the negative terminal of the battery supplies an equal amount of electrons to the plate connected to it giving it a surplus of electrons making the plate negatively charged.

In effect, there is no change in the total charge of the capacitor. Charge has simply been moved from one plate to another.

Now let's say the capacitor we just charged is your upper capacitor, but it is not yet connected in parallel to the lower capacitor. What will happen if we connect them in parallel? Well, that will depend on the capacitance of the two capacitors and whether or not the lower capacitor has been charged. Let's assume the lower capacitor is initially uncharged. Here's what we know will happen:

1. The upper capacitor will charge the lower capacitor until the potential difference for each capacitor is the same. (Generally the charging is through a resistor to limit potentially damaging high currents).

2. Because total charge has to be conserved, the sum of the charges on the two capacitors will have to equal $Q_1$, the initial charge of the upper capacitor. So, if $Q_U$ and $Q_L$ are the final charge on the upper and lower capacitors, respectively, $Q_{U}+Q_{L}=Q_1$

3. Since the final voltage on the two capacitors has to be the same, lets call it $V_f$, we have the final conditions of

$$Q_{U}=C_{U}V_f$$ $$Q_{L}=C_{L}V_f$$ $$Q_{U}+Q_{L}=Q1$$

And

$$Q_{1}=C_{U}V$$

Where $V=$ 1 volt and $C_U$ is the capacitance of your upper capacitor.

Q3

Your textbook is correct that series capacitors must always have the same charge. But a simpler explanation is as follows:

Capacitors in series all have the same total current flowing through them, or $I_{T}=I_{1}+I_{2}=I_{3}=$etc. Therefore each capacitor will accumulate the same amount of electrical charge, $Q$, on its plates regardless of its capacitance. This is because the charge accumulated by a plate of any one capacitor must have come from the plate of its adjacent capacitor. Consequently, $Q_{1}=Q_{2}=Q_{3}=$ etc..

..if we go by this explanation then when two capacitors having equal and opposite charges on both plates are connected together then the charge redistribution should never occur because the net electric field inside the conductors connecting the two is 0 always ,isn't it?

When you say "connected together" I assume you mean taking two of those series capacitors and connecting them in parallel. If that's the case, if the two capacitors have different capacitance but the same charge, then their voltages will be different before being connected together because

$$V=\frac{Q}{C}$$

In which case the capacitor having the higher voltage will charge the capacitor of lower voltage, redistributing the charge until the voltages become the same.

Hope this helps.

Answer 7

Key concepts when dealing with capacitors in a DC circuit:

1. Charge is conserved, so the battery does NOT create or destroy any electrons.

2. The battery acts as a "pump" for electrons, and moves electrons around in the circuit. This means that for one capacitor in the circuit, the battery removes electrons from the positive plate and pushes them onto the negative plate, until the potential difference across the capacitor equals the emf of the battery. It also means that the net charge on the capacitor is zero. For capacitors in series, this means that the total number of electrons pushed onto the negative plate of each capacitor (aka the charge) must be equal.

3. For capacitors connected in parallel with no battery in the circuit (your drawing in question 1.2) charge will redistribute until the the negative plates are at the same voltage (usually arbitrarily assigned a value of zero volts) and the positive plates are at the same voltage. The amount of charge on each of the parallel plates will depend on plate area, spacing between plates, the dielectric between the plates, etc.