1

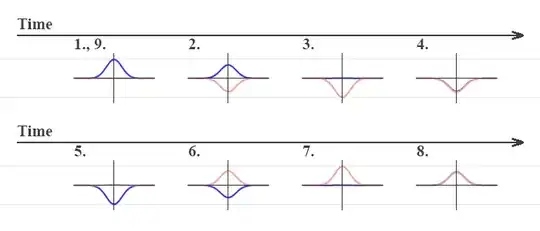
Here're key-frames from a time evolution of a quantum harmonic oscillator in it's ground state (source): enter image description here

So, I do understand that such a state may equally well describe grand variety of systems, but for now I want to focus on just 1 "particle on a spring" example, just to see if the following description will be all on itself valid:

Time Particle's position Particle's momentum (direction only)
$1., 9.$ $x_0$ (equilibrium point) $x_1$ (maximum stretching)
$3.$ $x_1$ $x_{-1}$ (maximum compression)
$5.$ $x_0$ $x_{-1}$
$7.$ $x_{-1}$ $x_1$

Btw, I do understand also that:

  • these $x$ points are arbitrary: we could've started at any other point than $x_0$ (with it's role as "equilibrium point" unchanged), and $x_1$ and $x_{-1}$ roles might've been swapped.
  • measuring upon the system in the table would not have revealed a "particle" in it's $x$ position (with described momentum), but rather in any of possible outcomes.

I'm just interested in validity of meaning I've put in that table - say, as a time evolution of just 1 eigenstate.

Victor Novak
  • 199
  • 1
    What are $x_0$, $x_1$, etc.? Anyway, what you've written in the table is not correct, because a particle in an eigenstate of the harmonic oscillator hamiltonian does not have a definite position or momentum. I'm also confused what the title of the question has to do with the body. – d_b Jun 25 '21 at 02:42
  • What are $x_0$, $x_1$, etc. can be seen (in round brackets) in a table. Please make sure you've read "Btw" section under the table to be on the same page with me about my usage here of an eigenstate term. – Victor Novak Jun 25 '21 at 02:45
  • Given your second bullet point ("measuring upon the system...") I don't know how to interpret the columns of the table. What do you mean specifically by "Particle's position" if not "the position we would measure for the particle"? – d_b Jun 25 '21 at 03:00
  • @d_b well, yeah... may be just a "thought interpretation" of a time evolution - as if we could apply Schrödinger equation on classical particle. Here's description of a table: $1., 9.$: particle starts at $x_0$ (equilibrium) with it's momentum pointing at $x_1$ (maximum stretching). $3.$: particle reaches $x_1$ with it's momentum now pointing at $x_{-1}$ (maximum compression). $5.$: particle returns to $x_0$ with it's momentum still pointing at $x_{-1}$. $7.$: particle reaches $x_{-1}$ with it's momentum now pointing at $x_1$, and repeat. – Victor Novak Jun 25 '21 at 03:13
  • @d_b So, given the "Btw" points, the question was, do I read imaginary and real parts of a wave function correctly? Now I see from Sandejo's answer that there're many layers differing quantum from classical, even with the "Btw" points. – Victor Novak Jun 25 '21 at 03:26
  • Most notable difference is Sandejo's point on "energy eigenstate", which, of course, limits possible momenta. – Victor Novak Jun 25 '21 at 03:49

2 Answers2

3

In quantum mechanics, particles do not have well-defined positions or momenta. Instead, we can only talk about the probability distribution we would get if we measured them. These probability distributions are given by the Born rule, which says that the squared norm of the wavefunction (expressed in the basis of the variable being measured) is the probability density function for the measurement of that variable. For example, the probability of measuring the position to be in some interval $[a,b]$ is given by $\int_a^b\mathrm{d}x\,\lvert\psi(x)\rvert^2$.

When a state is an eigenstate of the Hamiltonian, such as the ground state, it is called a stationary state. This is because its time evolution is entirely given by a phase factor: $\psi(x,t)=e^{-iEt/\hbar}\psi(x,0)$, where $\psi(x,0)$ is an eigenfunction with energy eigenvalue $E$. Notably, when you take the squared norm, the time dependence vanishes, since $\lvert e^{-iEt/\hbar}\rvert^2=1$, meaning the probability distributions for measurements are the same at any time. Therefore, it does not make sense to think of a particle in a quantum harmonic oscillator as moving back and forth, analogous to a classical harmonic oscillator. In particular, the particle effectively does not change if it is in an energy eigenstate. However, if the particle is not in an energy eigenstate (instead being in a superposition of states with different energies), then the expectation values of the position and momentum will oscillate similar to the classical case.

Sandejo
  • 5,478
2

As has already been said by Sandejo, the position and momentum do not have well-defined values for a quantum particle. However, it is possible to relate the behavior of the quantum particle with that of a classical particle by considering the expectation values of the position and momentum operators in the state of interest.

For the quantum harmonic oscillator, the expectation value of both position and momentum are zero at all times in an energy eigenstate, so from this point of view the motion of the quantum particle does not resemble at all the back-and-forth motion that you expect from a classical oscillator.

As also said by Sandejo, a superposition of energy eigenstates could lead to time-dependent position and momentum expectation values. At this point, it is interesting to ask the question of which quantum states would lead to a motion that most closely resembles the behaviour of the quantum harmonic oscillator. The answer is something called coherent states, typically labelled with $|\alpha\rangle$. They can be defined in a variety of ways (e.g. as the eigenstates of the lowering operator: $\hat{a}|\alpha\rangle=\alpha|\alpha\rangle$), and in the energy basis they take the following form:

$$ |\alpha\rangle=e^{-|\alpha|^2/2}\sum_{n=0}^{\infty}\frac{\alpha^n}{\sqrt{n!}}|n\rangle, $$

where $|n\rangle$ are the energy eigenstates. For these states, the expectation values of the position and momentum operators exactly follow the classical trajectories.

ProfM
  • 1,193
  • 6
  • 10