I was reading brief history of time by hawking and there I stuck on this line
“A theory is a model of universe or a restricted part of it and a set of rules that relate quantities in the model to observations we make.”
What is it saying? Please elaborate. What are rules and quantities?
Also
“You can disprove a theory by finding even a single observation that disagree with the predictions of the theory.”
What is this prediction?
“A theory is a model of universe or a restricted part of it and a set of rules that relate quantities in the model to observations we make.”
What is it saying? Please elaborate. What are rules and quantities?
So, let me start with something that's closer to the everyday experience. Say that every time you enter a certain menu in an app on your phone, the phone becomes non-responsive, and apparently blocks.
You get frustrated, and you start clicking various physical buttons available on the side frame, and you discover that if you click the "Volume Up" button a number of times, the phone eventually unblocks.
Hm... so now you have a small theory (in an informal sense of the word) that describes a rule about how something works: "If the phone gets blocked after entering this particular menu, repeatedly clicking the 'Volume Up' button causes it to unblock."
It's a description of a real-world phenomenon you encountered; a description of a particular aspect of a "restricted part of the universe" that is your phone.
“You can disprove a theory by finding even a single observation that disagree with the predictions of the theory.”
What is this prediction?
Now, if you think about it, you can't really be 100% sure that your theory is correct. E.g. while it's possible that pressing the "Volume Up" button does something that somehow unblocks the phone, it's also possible that the software in the phone gets confused for a bit, and then sorts itself out and continues working normally after a while, so the phone simply unblocks itself on its own, and you pressing the "Volume Up" button has nothing to do with it. It's just a ritual you do. Or maybe it's something completely different - perhaps getting a direct message in some other app while the phone is blocked, causes the blocking app to crash, which unblocks the phone. Or it's something else entirely.
Well, while you can't be 100% sure, you can do some tests to increase your confidence in your conclusion - or reject your theory if the tests invalidate its predictions. So, what are it's predictions? A prediction is anything that the theory says will happen according to its rules if you do some kind of experiment, if you "poke" the system in some way. Yours is not a very complicated theory, so it doesn't have a lot of predictions. One of them is that clicking the "Volume Up" button repeatedly unblocks the phone under the described circumstances. Another is more interesting from the perspective of experimental check:
So you set up an experiment: you enter the problematic menu, and leave your phone alone for some time. Say you come back 10 min later, and you discover that your phone is working just fine! Well, then, that means that your theory was wrong, there's no way around it!
Now, this same sort of thing happens when it comes to our scientific understanding of the world. However, scientific theories are usually more expansive frameworks, with more "moving parts", and are significantly more formal and more precise.
For example, the problem with saying "if you click the 'Volume Up' button a number of times" is that it's not very clear what that means. Is it enough to click two or three times? Can you conclude that the theory is wrong if you click 20 times, and nothing happens? Perhaps sometimes it takes about 500 clicks, because of something that happens internally in the phone that causes the number to vary wildly.
Suppose now that the "phone unblock theory" is true. You could improve it by performing lots of experiments and then putting some numbers in it. Maybe you can come up with an upper bound: "it takes < 10 clicks". Or maybe you're able to determine the exact number of clicks. Now all of a sudden you have things in your theory that are quantifiable. You can measure and/or count things and produce inferences based on that.
Another thing to note here is that the "phone unblock theory" describes this behavior of the phone in a "high level" way; it doesn't actually describe the underlying mechanism that unblocks the phone. For that, you'd need to understand how the internal details of the phone work, how its hardware and software components interact. In other words, you'd need a deeper, more fundamental "low level" theory that captures your understanding of the inner workings of the phone, and a way to relate it to the more high level theory you started with - to show how the high level theory emerges from the more fundamental one.
“A theory is a model of the universe or a restricted part of it"
The word "model" just means "a representation", "a description". It's a "model" because, while it captures some aspect of reality (describes some structure and/or behavior, relates some elements together, talks about rules and quantities), it's always different from the real thing in some way.
Consider a bust, a three-dimensional clay model of a person; it captures someone's likeness, but ignores details deemed less important or irrelevant for the artist's purpose. E.g. it represents the shape of the face, and even wrinkles, but not small pores, or individual strands of hair, or internal organs, or the fabric of the clothing, or even color of anything.
It's a strategic simplification of the real thing; an abstraction of something concrete.
So is every scientific model. There are always assumptions made, and things that are ignored, aspects of the phenomenon that are deemed unimportant for the core problem, effects that are considered irrelevant. So you always have to keep in mind that, if you're trying to understand some real-world phenomenon using any theoretical framework, there are assumptions that are being made, and check if those assumptions are reasonable for the real-world problem you're dealing with.
How this manifests in science? For example, consider the exponential growth curve that describes how population size changes over time - e.g. a number of water lilies in a pond. It's a theoretical model capturing the essence of the scientific understanding of how populations grow. It involves a certain formula that relates time and population size, and or quantities like the current population size and future population size. It produces a curve like the one below. It comes with the premise that the exact number of individuals is not all that important, and what the model cares about is the overall trend; it comes with the understanding that if for day 5 the formula outputs the number 9.73, it doesn't mean that there's somehow 9.73 water lilies, but that there's 9 or 10 fully formed individuals. It involves an assumption that for the duration of interest the water lilies don't run out of space to expand (there's always more than enough pond left uncovered).
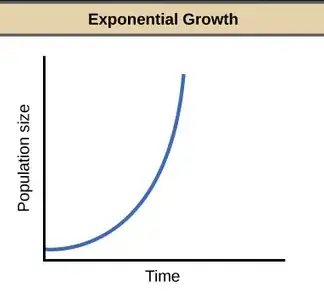
It also involves an understanding that if the assumption that there's always enough free surface left in the pond is wrong, then the model is not applicable (or is only applicable in for the initial time period - there, it's "good enough"). The fact that the resources are now limited affects the curve, and at some point the original model starts giving wrong predictions (it significantly overestimates the population size).
To take such circumstances into consideration as well, a more general, more accurate model is needed. And so there's a different formula that better captures what's actually going on:
But this is still a model, a strategic simplification of the more complicated reality.
A "law" has no special meaning/status in science. It's not used to denote an unassailable truth. The word "law" is just a synonym for "rule", "formula". Some "laws" are only approximate, some are better established than others, some are so well established they are considered fundamental. But it's all ultimately models.
Well, it's just a formula describing how gravity works, being a part of the overall Newtonian theory of gravity. And today we know it's not exactly right. It's superbly accurate for everyday scenarios, but it starts to break down in circumstances involving things like black holes - in those regimes, it stops producing correct predictions, the calculations produce results that don't closely match what's actually observed.
That's the whole reason why we have the theory of general relativity, which is a more fundamental, more encompassing theory of gravity, which, by the way, reduces to — or matches — Newtonian gravity in non-relativistic scenarios. You don't throw away what worked before; you throw away the parts that were wrong, and produce a refinement.
All of science is built on such models; it's ideally built on falsifiable theories, that you can experimentally test in different ways to increase your confidence in the theoretical description, or find out what aspects of it are wrong, and where the boundaries of its applicability are. Some aspects of a scientific theory will be firmly supported by experiments, others will be on the frontier of our knowledge and technology, and some will be beyond our technological capability. Other aspects will be of a more conceptual nature, and will be more a reflection of how we think about things, rather than of the underlying structure. You can have more than one theory of the same phenomenon that conceptually describe it in different ways, and go about establishing their formal mathematical structure and formulas differently, but ultimately give the same predictions. Or you can have theories that mostly give the same predictions, except for a few things that we haven't been able to check yet - enabling us to eventually establish which of the two theories is more generally correct.
On their own, facts are just data - and you can't really do anything with data unless you have some interpretative framework that puts it into context, that offers you some perspective from which you can understand what the data means. A scientific theory is such an interpretative framework, "battle tested" through various experimental checks it has been subjected to, with all the caveats about assumptions made, about applicability, and about known and unknown limits, that go with the scientific approach.
P.S. As further illustration, read about the History of Atomic Theory here (you can skip the first part if you want, and start with Brownian Motion section). Note how throughout history scientists had different theoretical models of the atom, refining it along the way as new discoveries are made. Every model was in a sense wrong (it didn't precisely capture what the real atom is like), but every model was also, in a different sense, right, or at least useful (it captured correctly some aspect of the atom, in a more abstract way). And every refinement made the model more correct, or gave it more explanatory power. There's no reason to think that the current model of the atom isn't missing some even more fundamental aspect that we don't yet know about.
One of the best ways of understanding his definition of a theory, is to compare his definition with any of the current theories in physics.
For example, if you consider the Special theory of Relativity and see how it relates to each part of the definition used by him
"A theory is a model of universe or a restricted part of it"
Special theory of relativity is a model that is restricted to the macroscopic scale i.e. to the objects in universe greater than the nano-scale of sub atomic particles.
"set of rules that relate quantities in the model to observations we make" .
In the model of special theory of relativity, the quantities of the model are the lengths of objects, time intervals between events, space and time coordinates of events etc.
And the set of rules are the rules of time dilation, length contraction, lorentz transformation etc. We use these rules to relate the quantities in the model to observations we make in the real world.
So, for instance in the real world, we observe time dilation in high speed experiments. The rules of time dilation allow us to relate these observations to the quantities in the model. Without the theory of special relativity , we would not be able to explain these observations of the real world experiments.
“You can disprove a theory by finding even a single observation that disagree with the predictions of the theory.”
The predictions refer precisely to what these rules predict about observations in the real world. In special theory of relativity, the rules of time dilation , predict that moving clocks tick slower. The rules of length contraction predict that moving lengths contract. There are a few other such rules that predict few other things as well. If we are able to find even a single verified observation in the real world that disagrees with these predictions, then the theory would have been disproven, and would either have to be modified or discarded completely
In general, experiments in the real world have two distinguished sets of information: inputs and the outputs.
For example, if you want to know how long you can drive your car for before it runs out of fuel, you are going to have broadly two sets of information:
Inputs: Mass of car, friction of tires, air resistance, details about how efficient the engine is etc.
Outputs: The distance the car travels before it runs out of fuel.
The job of the scientist is then to find a mathematical formula which, given the numerical set of inputs, produces the correct numerical output.
Note that, even though it sounds a bit obvious to say, any old formula doesn't work. If you simply multiply the quantities together, you probably won't get the correct result. However, once you know the correct formula, it should in principle be able to predict the outcome of any such similar experiment (e.g. with a different car under different driving conditions) assuming you enter the input data correctly each time.
This is a very general setup, and applies even when we have no idea what is actually happening between the input and output data. For instance in a particle collider, the input information would be the types of particles, how fast they are travelling, the direction in which they are travelling etc. and the output data would be similar information about the outgoing particles. The only purpose of the mathematical theory itself is to correctly predict the output data given the input. Zero knowledge of the intermediate processes are required and in fact it is a common source of confusion among non-physicists to try to interpret mathematical intermediate steps with physical intermediate steps, as tempting as it is, this often causes problems particularly in more advanced physics.
Let's take Newtonian gravity as an example. Newton's theory of gravitation is that there is an attractive force between any two objects $m_1$ and $m_2$ separated by a distance $r$, which points along the line connecting the two objects, and whose magnitude is \begin{equation} F = G\frac{m_1 m_2}{r^2} \end{equation} where $G$ is Newton's constant.
Given this law, as well as Newton's law of motion $F=ma$, we can set up a system of differential equations and solve them to find how a collection of objects will move under the influence of gravity.
This system of equations is a model. Let's see how Hawking's general comments apply to this specific example.
I want to close by emphasizing that above I have only given a specific example to illustrate the main points, but Hawking's comment is much more general and can be applied in many different situations not involving gravity at all.
