Can information be analog?

Question

In connection with question What do physicists mean by "information"? I read "information" simply means any particle, feature of in a field (EM, quantum field, curvature in spacetime ...), message or so forth that could allow a causal link between A and B, i.e. could make B's physics depend on A's presence (and contrariwise)."

From this, it seems to me that information is not necessarily digital-wise. For example, if we change the position of body A, body B experiences the change. In a classic direct momentum transfer (collision), the causal link exists, the collision creates/transfers information and the momentum is the transferred 'information'. It is partly digital (if collision occurred), part of if (the amount of momentum exchanged) are analog. Can we interpret information transfer to this case?

Answer 1

What we mean by "information" started in the seminal paper by Claude Shannon, A mathematical theory of communication. Shannon gave a generalized picture of communication which is shown schematically in Fig. 1 of this paper (reproduced below) and consists of effectively three stages; a sender and receiver (traditionally named Alice and Bob), and a physical medium or channel over which the intended information is transmitted between Alice and Bob.

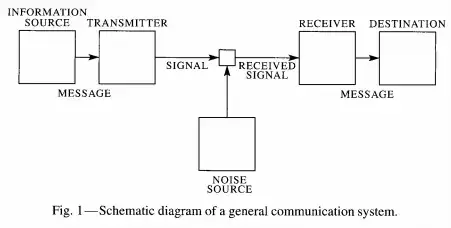
Alice must encode the intended information onto some physical medium that can be transmitted to Bob. This stage is the fundamental stage of abstracting or symbolically representing meaning. Language is a natural example of this. In speech a specific idea is represented by a specific sound or grouping of sounds, while in written language the representation of the idea is in the form of visual characters or symbols. In general, ideas are represented in some physical form that can be transmitted and ultimately experienced or sensed by another person. Each physical symbol is chosen from a set of distinct possible symbols with pre-agreed upon meanings. Note, this process is inherently discrete given the requirement of having a countable number of possible pre-agreed upon messages (i.e. a pre-agreed upon language/alphabet)!

So in the general communication scheme of the figure above, Alice translates the intended message into a series of abstract symbols. Each symbol is encoded onto the state of the physical medium in one of a number of different possible configurations. The list of possible configurations or symbols $x\in \mathbb X$ is called the alphabet, in analogy with written communication. The information $I(X)$ of a random symbol $X$ with $N$ equally likely possible values $x\in\mathbb X$ is defined to be

$$I(X) = \log_b(N).$$

The logarithmic measure of information is chosen because the number of distinct possible messages generally grows exponentially with resources. For example if a message contains $n$ independent random symbols $X$, each chosen from an alphabet of size $N$, then the total number of possible combinations of sequences is $N^n$, and the amount of information contained in this sequence is

$$I(X^n) = \log_b(N^n)=n\log_b(N) = n I(X).$$

It should be noted that information as defined above is only defined to within a constant, which is equivalent to the freedom to choose the base $b$ of the logarithm which defines the units of information. If the natural logarithm is chosen then information is given by nats, if base 10 is chosen the information given is in Hartleys, and of course if base two is chosen then the information is in the familiar bits.

The second piece of the puzzle comes from Shannon's Noisy-channel coding theorem. This theorem establishes that for any physical channel there is a maximum rate of discrete data that can be encoded, even if the physical medium is continuous (e.g. analog)! This maximimum rate is known as the channel capacity. The hand-wavy way to think about this is every physical quantity will always have a finite (e.g. countable/discrete) resolution. For instance, imagine you are trying to communicate via the time varying voltage sent along a coaxial cable. The maximum useful size of your alphabet might be encoded on the magnitude of the voltage at any moment in time. Although voltage may be physically continuous (e.g. there are an uncountable infinite number of voltages between say 0 and 1 volt), your ability to resolve the voltage is not. So you may be able to distinguish 0 from 1 volt, but not 0 from 0.001 volts. The finite number of voltage levels (set by e.g. this resolution and the maximum energy/voltage you're willing/able to use) then gives you the capacity of that channel to encode information. The number of symbols you use (i.e. the number of distinguishable physical states) must then be less than or equal to this number if you want to communicate without error.

Answer 2

The main reason we store information as bits on digital computers is robustness.

In a typical circuit, a "one" is defined as the presence of some voltage across two points in a circuit, and a "zero" is defined as the absence of the voltage.

Of course voltage is actually a continuous quantity, so in principle we could store an arbitrarily large amount of information in it! For example, let's say our voltmeter can measure voltages up to $10\ {\rm V}$. Instead of saying "zero" means that the potential difference is less than $5\ {\rm V}$ and "one" means the potential difference is more than $5$, we could say "zero" means less than $3\ {\rm V}$, "one" means between $3\ {\rm V}$ and $6\ {\rm V}$, and "two" means greater than $6\ {\rm V}$. By subdividing this interval into finer and finer steps, we could store more and more information in one circuit component.

In practice, this quickly becomes an engineering nightmare. There are measurement uncertainties and there are noise sources that can cause the voltage to change randomly and uncontrollably. Furthermore, properties of circuits tend to drift over time due to factors like temperature, usage, and electromagnetic effects in the environment. So it is much more robust to store only a small amount of information in an individual physical component of a circuit, and to build up a large information system by using many of these smaller information systems.

Tl;dr: Information is analog, in Nature. But real life is messy, so a major realization of the 20th Century is that we can build much more robust systems by digitizing the information, and chaining many simple digital components together, rather than using analog components.