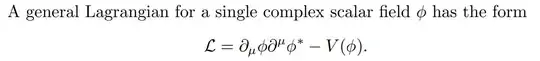I am wondering where this statement comes from.
I've tried to find out myself and just can't seem to figure it out. But it seems to be trivial everywhere that the kinetic term in the Lagrangian of a scalar field is the product of the derivatives.
Could someone help me understand this fact more?
The kinetic term has to be (i) a scalar and (ii) dependent on $\partial_\mu\phi$ so $\phi$ is dynamical, and (iii) can't simply contract this derivative with $\gamma^\mu$ as in a Dirac Lagrangian, since the scalar $\phi$ lacks a spinor's internal degrees of freedom. It must also be (iv) real, which is why the real-$\phi$ kinetic term $\tfrac12\partial_\mu\phi\partial^\mu\phi$ has complex-$\phi$ counterpart $\partial_\mu\phi\partial^\mu\phi^\ast$.
In theory, we could introduce a second scalar, say $\chi$, to get a kinetic term including e.g. a multiple of $\partial_\mu\phi\partial^\mu\chi$.That's not what we're "allowed" to do here, but see e.g. this question for a classical take on the consequences.
The other option is an $M(\phi)\partial_\mu\phi\partial^\mu\phi^\ast$ kinetic term, where $M$ is real. But you could use the chain rule to redefine $\phi$ so $M=1$, thereby changing the form of $V$, so that trick also "doesn't count".
Let's think about what you can do with zero derivatives, and one scalar field $\phi$. You can pretty much have any (analytic) function of $\phi$, which amounts to a potential $V(\phi)$. (There are also some stability constraints -- the potential should be bounded from below).
How about one derivative, $\partial_\mu \phi$? Well, if we want our theory to be Lorentz invariant, then $\mathcal{L}$ needs to be a scalar. There are no other tensors for $\partial_\mu \phi$ to contract with, so we can't do much here.
With two derivatives, we could write $Z(\phi) (\partial \phi)^2$. As pointed out in another answer, we can set $Z(\phi)$ to $\pm 1$ by a redefinition of $\phi$. What restricts the sign of the kinetic term is then stability. If you have a field with the "wrong sign" of kinetic energy -- so the kinetic energy is negative -- then your theory has developed a so-called ghost instability. This is a very bad instability, because the timescale over which the theory becomes unstable is arbitrarily small. Quantum mechanically, the vacuum is unstable to decaying into "ghost" particles and "ordinary" particles, with an infinite decay rate (provided your scalar field couples to other fields -- and at least we would expect it to couple to gravity).
You can also write $P(X)$, where $X=(\partial \phi)^2$ is the standard kinetic term. For example, you can have $P(X)=X+X^2$, or $P(X)=\sqrt{1-X^2}$ (the latter is called the DBI action). This class of theories is used in cosmology, and can describe different kinds of fluids. DBI describes the motion of a brane in a higher dimensional space.
What about higher derivatives than two? Due to a theory by Ostragradsky, if the equations of motion are higher than second order in time derivatives, then the theory develops a ghost instability and is unstable. There are a few ways out of this...
Putting this together, if you want to work with theories that are well-defined classically (without a cutoff) and stick to "mainstream" Lagrangians that avoid potential superluminality problems, the above considerations of Lorentz invariance, stability, and the constraints of working with one scalar field essentially limit you to the form you wrote down.
There are generalizations ($P(X)$ and Galileons) that are stable, but these are also somewhat more complicated to analyze, and since they are non-renormalizable they require some knowledge of effective field theory to understand from a quantum point of view, and additionally their relevance to physics is only in a narrow domain (compared to the good old ubiquitous "standard scalar field") and is speculative, so these cases are not taught in textbooks.
It comes from the Klein--Gordon equation, which is the relativistic equation for spin $0$ fields. If we consider the Lagrangian you provided with $V=0$, the Euler--Lagrange equations will return precisely the massless Klein--Gordon equation, hence reproducing the equation of motion of a free, massless spin $0$ field. Therefore, the kinetic term should be the product of the derivatives. One can then add a mass term and interaction by introducing terms in a potential $V$.
The given lagrangian provides the correct equations of motion once one varies the corresponding action with respect to the field $\phi$, in the same way the lagrangian
$$L = -\frac{1}{2}m \dot{x}^2 -U(x) $$
gives Newton's second law. You can see that in the lagrangian derivatives of the position field $x$ appear in order to obtain Newton's law which is a second order differential equation.
At a somewhat cursory level, it is often reasonable to assume Lorentz invariance of most physical systems of theoretical interest. So to start, we might ask what the most general theory would look like without this assumption. Recall that under Lorentz transformations, $x' = \Lambda x$, and the derivative of a scalar field transforms as
\begin{align*}
\partial'\phi(x') = \Lambda^{-1}\partial\phi(x)
\end{align*}
(In the terminology of differential forms, $\partial\phi$ contains the components of a 1-form, or a "covariant vector", in the sense that either $\partial'\phi(x') = \Lambda^{-1}\partial\phi(\Lambda^{-1}x')$, or $\partial\phi(x) = \Lambda\partial'\phi(\Lambda x)$, where the matrix on the left is the same as the matrix applied to the argument.)
In order to form a Lorentz scalar from $\partial\phi$, it is necessary to contract $\partial\phi$ with an ordinary 4-vector (or "contravariant vector"), like a 4-velocity or 4-momentum. There are essentially two ways that this can be done. First, one might choose an arbitrary 4-vector, $k^\mu$ say, and contract it with $\partial_\mu\phi$ to obtain $\partial_\mu\phi k^\mu$. Second, we could try to construct a 4-vector using $\partial_\mu\phi$ itself and the (inverse) metric $g^{\mu\nu}$, $\partial_\mu\phi g^{\mu\nu}\equiv \partial^\mu\phi$. This is how the $\partial_\mu\phi\partial^\mu\phi$ term arises in your example. The reason you don't see a $\partial_\mu\phi k^\mu$ term in the Lagrangian is that the $k^\mu$ term breaks Lorentz invariance of the theory. This is somewhat different from breaking Lorentz invariance of the Lagrangian (e.g. if instead of choosing a 4-vector $k$ we instead just picked a few random components of $\partial\phi$ (and powers thereof) to include in the Lagrangian, such as $(\partial_0\phi)^\nu$ or $(0.1\partial_1\phi + 0.3\partial_3\phi)^6$.) There are other ways in which the theory might break Lorentz symmetry. As it turns out, the metric $g_{\mu\nu}$ is the unique bilinear form that is preserved under (all) Lorentz transformations. Hence, if we replaced $g^{\mu\nu}$ in $\partial_\mu\phi\partial_\nu\phi g^{\mu\nu}$ with another rank-2 tensor, $M^{\mu\nu}=g^{\mu\rho}g^{\nu\sigma}M_{\rho\sigma}$ say, with off-diagonal elements or unequal diagonals, we would obtain another theory with a preferred frame (or set of frames: those in which the component matrix of $M$ is diagonal.)
At a less cursory level, it might be worth asking how a deviation from Lorentz invariance (whether in the theory or in the Lagrangian) would arise. Could it emerge from a scalar field, and if so, how?
