Where does pseudo force act at?

Question

It is known that, to apply Newton's laws in a non-inertial frame, we use the concept of pseudo force. We also know that force is a bound vector. Hence, is there a general way to determine where the pseudo force vector would be located at?

Answer 1

Pseudo-forces are determined by the acceleration of the reference frame and generally act at all points in space. For a linearly accelerating frame, the resulting pseudo-force is uniform. For a rotating reference frame the force depends on things such as the distance from the rotation axis, the speed of the rotation. The Coriolis force acting on a point particle also depends on the velocity of the particle relative to the rotating frame, but this effect still exists at all points in the rotating reference frame.

If you want to "condense" these forces to single points and moments for an extended object then you just have to find the weighted average of these quantities like you would for any other distributed load. Note that you need to do this separately for forces and torques; it's not true in general that the weighted average of the torques is equal to the torque of the weighted average of the forces.

Answer 2

Like gravity, pseudoforces apply at all points in a body. In mechanics, when we say that a distributed force "acts" at a single point, we mean that performing such a replacement does not change the torque acting on the body as a whole. Whether this is possible depends on the pseudoforce.

• In a uniformly accelerating frame, the pseudoforce can be taken to act at the center of mass of the body, with strength $M \mathbf{a}$.
• In a uniformly rotating frame, the centrifugal pseudoforce can be taken to act at the center of mass of the body, with strength $M \omega^2 \mathbf{r}_{\mathrm{cm}}$.
• The Coriolis force generally cannot be treated in this way. For example, there are situations where the total Coriolis force vanishes, but the total Coriolis torque doesn't.

Answer 3

In a linearly accelerated reference frame the same pseudo force acts uniformly (at any given instant) on all particles in an extended body. This set of pseudo forces can be replaced by a single force acting at the body’s centre of mass.

In a rotating reference frame the pseudo forces will not be uniform, so you have to determine the pseudo force acting on each particle individually and then integrate across the body as a whole.

It is no coincidence that this parallels the analysis of the motion of an extended body in a uniform or non-uniform gravitational field.

Answer 4

Summary

Consider a system of particles, not necessarily a rigid body, as viewed in an inertial frame. The translational motion (the change in total linear momentum) can be evaluated assuming the total mass is a particle located at the center of mass (CM) acted on by the total external force. The rotational motion (the change in angular momentum) cannot be evaluated assuming the total external force acts at the CM.

As viewed in a non-inertial frame, the above conclusions apply but in addition to the external forces, fictitious forces need to be considered. The translational motion (the change in total linear momentum) can be evaluated assuming the total mass is a particle located at the center of mass (CM) acted on by the total external force plus the total fictitious force. The rotational motion (the change in angular momentum) cannot be evaluated assuming the total external force of the total fictitious force acts at the CM.

Here is a simple example. Assume a rigid rod is supported by a pivot at its CM, and is acted on by a force $F$, downward at a distances $d$ to the right of the CM. The CM is stationary. Viewed in the inertial frame, this force produces rotational motion about the CM. Now consider the motion as viewed in a non-inertial, rotating frame in which the rod is at rest. In this frame, fictitious forces counter $F$ force to keep the rod at rest. If the fictitious forces were assumed to act at the CM they could not keep the rod stationary in the non-inertial frame. Certain forces can be assumed to act at the CM. The force of gravity and the fictitious force that arises from translational acceleration can be assumed to act at the CM. Consider the rigid rod free to fall with gravity the only applied external force. In the inertial frame the rod falls but does not rotate about its CM since gravity can be assumed to act at the CM. In the non-inertial frame in which the rod is the rest, the fictitious force that keeps the rod stationary acts at the CM and there is no rotation about the CM.

A more detailed discussion for translational and rotational motion follows.

Translational and Rotational Motion in Inertial Frame

Consider a system of particles, not necessarily a rigid body. See Figures 1 and 2.

In an inertial system, the translational motion can be evaluated assuming the total mass is located at the center of mass (CM). The total linear momentum $\vec P = ∑_{i=1}^{k} m_i\vec v_i = M \vec V$ where $m_i$ is the mass of each particle with velocity $\vec v_i$, $M = ∑_{i=1}^{k}m_i$ is the total mass, and $\vec V$ is the velocity of the CM. $M \vec A = \vec F_{tot}{^{ext} }$ where $\vec A$ is the acceleration of the CM and the total external force $\vec F_{tot}{^{ext}} = ∑_{i=1}^{k}\enspace \vec F_i^{\,ext}$ is the sum of the net external force on each particle.

The rotational motion about a point cannot be considered assuming the total mass is located at the CM; the rotational motion depends on the specific locations on the body where the external forces are applied. The total angular momentum about a point $Q$ is $\vec L_Q = ∑_{i=1}^{k}\enspace \vec r_{iQ} \times m_i \vec v_i$, where $\vec r_{iQ}$ is the position of $i$ with respect to $Q$. The change in angular momentum of the system about a point $Q$ is ${d \vec L_Q \over dt} = \vec N_Q^{\,ext} - \vec v_Q \times \vec P$ where $\vec v_Q$ is the velocity of $Q$ and $\vec N_Q^{\,ext} = ∑_{i=1}^{k}\enspace \vec r_{IQ} \times \vec F_i^{\,ext}$ is the total torque from external forces. [Kochmann] If $Q$ is chosen as the CM, the $\vec v_Q \times \vec P$ term is zero. Only for certain forces, such as gravity, can the forces be assumed to act at the CM for evaluating the rotational motion.

As subsequently discussed, similar conclusions hold in the non-inertial system if the fictitious forces are also considered. the translational motion can be evaluated assuming the total mass is located at the center of mass (CM). The rotational motion depends on the specific locations on the body where the external forces are applied.

Translational and Rotational Motion in Non-Inertial Frame

For a system of particles, the motion of the center of mass in a non-inertial reference frame is due to the total external force in the inertial frame plus the following fictitious forces: centrifugal force, Coriolis force, Euler force, and the force from translational acceleration of the non-inertial frame.
Consider a system of $k$ particles from the perspectives of both an inertial and a non-inertial frame of reference with respective origins at O and O*. O is stationary and O* is in acceleration with respect to O and the Cartesian axes for O* rotate with respect to those of O. CM denotes the position of the center of mass of the particles. As derived in physics mechanics textbooks, for a single particle in the system of particles [Symon] $(1) \enspace m{d^{*2} \vec r^{\, *} \over dt^2} = m( {d^{2}\vec r \over dt^2 }- \vec \omega \times (\vec \omega \times \vec r^{\,*} )- 2\vec \omega \times {d^*\vec r^{\,*}\over dt}- {d \vec\omega \over dt}\times \vec r^{\,*} - {d^2\vec h \over dt^2 })$

$(2)\enspace m{d^{*2}\vec r^{\,*}\over dt^2 }$ is the acceleration of the particle in the non-inertial frame.

$(3)\enspace m {d^{2} \vec r \over dt^2} = \enspace \vec F^{\,ext} + \vec F^{\,int}$ Is the acceleration of the particle in the inertial frame
where $\vec F^{\,ext}$ is the net external force on the particle, and $\vec F^{\,int}$ is the net internal force on the particle from other particles.

$(4)\enspace - m\vec \omega \times (\vec \omega \times \vec r^{\,*})$ is the centrifugal force on the particle in the O* frame.

$(5)\enspace- 2mω \times {d^*\vec r^{\,*}\over dt}$ is the Coriolis force on the particle in the O* frame.

$(6)\enspace -m {d \omega\over dt}×\vec r^{\,*} $ Is the Euler force on the particle in the O* frame.

$(7)\enspace -m{d^2\vec h \over dt^2}$ is the fictitious force from the translational acceleration of O* with respect to O.

Summing overall particles in the system using Eqn. 1 , we have

$(8)\enspace ∑_{i=1}^{k} m_i{d^{*2} \vec r_i^{\,*} \over dt^2} = ∑_{i=1}^{k} m_i( {d^{2} \vec r_i \over dt^2} - \vec ω×(\vec ω×\vec r_i^{\,*}) - 2\vec ω×{d^* \vec r_i^{\,*} \over dt} - {d \vec ω\over dt} ×\vec r_i^{\,*} - {d^2 \vec h \over dt^2})$

$(9)\enspace ∑_{i=1}^{k} m_i {d^{2} r_i \over dt^2}=\sum_{i=1}^{k}\vec F_i^{\,ext} + \vec F_i^{\,int} = \sum_{i=1}^{k}\vec F_i^{\,ext} $ since the total internal force is zero based on Newton’s third law. See Figure 2. Note that the distance from the CM to particle $i$ is $\vec r_{iCM}$ in both the O and O* frames. For a rigid body, the magnitude of $\vec r_{iCM}$ is constant in the inertial (and non-inertial) frame.

$(10)\enspace \vec r_i^* = \vec R^* + \vec r_{iCM}$ where $\vec r_i^*$ is the location of particle $i$ in the O* frame with respect to O*, $\vec R^*$ is the location of the CM in the O* frame, and $\vec r_{iCM}$ is the location of particle $i$ with respect to the CM. Therefore,

$(11) ∑_{i=1}^{k}\enspace m_i\vec r_i^* = ∑_{i=1}^{k}m_i\vec R^* + ∑_{i=1}^{k}m_i\vec r_{iCM}$.

By the definition of the CM

$(12)\enspace ∑_{i=1}^{k} m_i \vec r_i = MR$ where $M= \sum_{i=1}^{k} m_i$ is the total mass.

Using Fig. 1,

$(13)\enspace MR = \sum_{i=1}^{k} m_i \vec r_i =\sum_{i=1}^{k} m_i (\vec R + \vec r_{iCM}) = MR + \sum_{i=1}^{k} m_i \vec r_{iCM}$, therefore

$(14)\enspace \sum_{i=1}^{k} m_i \vec r_{iCM} = 0$ and Eqn. (11) reduces to

$(15)\enspace \sum_{i=1}^{k} m_i \vec r_i^* = M\vec R^*$ where $\vec R^*$ is the location of the CM in the O* frame.

Using Eqn. (15),

$(16)\enspace \sum_{i=1}^{k} m_i \vec v_i^* = M\vec V^*$ and

$(17)\enspace \sum_{i=1}^{k} m_i \vec a_i^* = M\vec A^*$ Where V* and A* are the velocity and acceleration, respectively, of the CM in the O* system.

Using Eqns. (9), (15), (16), and (17) in Eqn. (8), we have

$(18)\enspace M\vec A_{CM}^{\,*} = \vec F_{total}^{\,ext} -M\vec \omega \times(\vec \omega \times \vec R_{CM}^{\,*}) - 2M\vec \omega \times \vec V_{CM}^{\,*} - M{d\vec \omega \over dt} \times \vec R_{CM}^{\,*} - M\vec a_O^{\,*}$ where $\vec F_{total}^{\,ext} = \sum_{i=1}^{k}\vec F_i^{\,ext}$ and $\vec a_O^* = {d^2 \vec h \over dt^2}$ is the acceleration of O* with respect to O.

The left hand side of Eqn. (18) is the total force on the CM in the non-inertial O* frame. The first term on the right hand side is the total external force in the inertial frame. The second, third, and fourth terms on the right hand side are, respectively: the total centrifugal force, the total Coriolis force, and the total Euler force. The last term on the right hand side is the fictitious force arising from the translational acceleration of O*. Relationship (18) is also provided in a reference. [Kochmann]

Note that the net centrifugal, Coriolis, and Euler forces can be expressed in terms of the total mass and the location and movement of the CM in Eqn. (18), and the total fictitious force from the translational acceleration of O* can be considered to act at the CM.

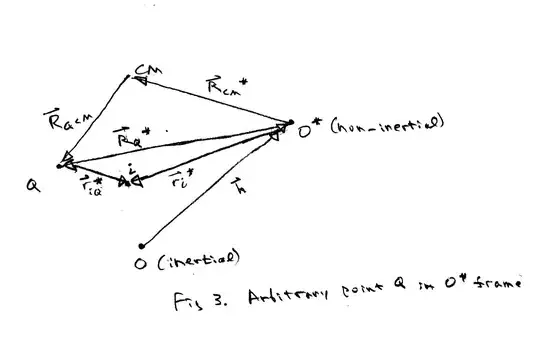
Now consider the rotational motion in the non-inertial frame. See Figure 3.

With respect to Q, in the non-inertial frame the total angular momentum is $$(19) \enspace\vec L_{Q}^{\,*} = \sum_{i=1}^{k}m_i\vec r_{iQ}^{\,*} \times \dot {\vec r}_i^*$$ Using $\vec r_{iQ}^{\,*} = r_i^{\,*} - R_Q^{\,*}$, the derivative of the total angular momentum is ${d\vec L_{Q}^{\,*} \over dt } = \sum_{i=1}^{k}m_i \vec r_{iQ}^{^\,*} \times \vec a_i^{\,*} + \sum_{i=1}^{k}m_i \dot {\vec r_{i}}^{*} \times \dot {\vec r_{i}}^{\,*} - \dot {\vec R_{Q}}^{*} \times \sum_{i=1}^{k}m_i \dot {\vec r_{i}}^{*}$ where $\vec a_i^{\,*}$ is the acceleration of particle $i$ in the non-inertial frame. The second term on the right hand side is zero.

$M \vec R_{CM}^* = \sum_{i=1}^{k}m_i r_i^*$ where $\vec R_{CM}^*$ is the position of the CM in the non-inertial frame. $ \vec P^* = \sum_{i=1}^{k}m_i\vec v_i^{\,*} = M\vec V^*$ is the total linear momentum in the non-inertial frame where $\vec V_{CM}^*$ is the velocity of the CM in the non-inertial frame. $\dot {\vec R_{Q}}^{*} = \vec v_Q^{\,*}$.

Therefore, $$(20) \enspace{d \vec L_{Q}^{\,*} \over dt } = \sum_{i=1}^{k}m_i (\vec r_{iQ}^{^\,*} \times \vec a_{i}^{\,*}) - \vec v_{Q}^{\,*} \times \vec P^*$$ Using Eqn (1) for $m_i\vec a_i^*$ we have

$$(21) \enspace{d \vec L_{Q}^{\,*} \over dt } = \sum_{i=1}^{k}\vec r_{iQ}^{\,*} \times (\vec F_i^{\,ext} + \vec F_i^{\,cent} + \vec F_i^{\,corio} + \vec F_i^{\,Euler} + \vec F_i^{\,trans})$$

$\vec F_i^{\,ext} $ is the total external force on particle $i$.

$\vec F_i^{\,cent} = - m_i\vec \omega \times (\vec \omega \times \vec r_i^{\,*})$ is the centrifugal force on the particle in the O* frame..

$\vec F_i^{\,corio} = - 2m_i \vec \omega \times {d^*\vec r_i^{\,*}\over dt}$ is the Coriolis force on the particle in the O* frame.

$\vec F_i^{\,Euler} = - m_i {d \vec \omega\over dt}×\vec r_i^{\,*}$ is the Euler force on the particle in the O* frame.

$\vec F_i^{\,trans} = -m_i{d^2\vec h \over dt^2}$ is the fictitious force from the translational acceleration of O*.

The torque with respect to $Q$ from the total fictitious force due to the translational acceleration of $O^*$ is $\sum_{i=1}^{k}\vec r_{iQ}^{\,*} \times (-m_i{d^2\vec h \over dt^2}) = \sum_{i=1}^{k}m_i(\vec r_i^* - \vec R_Q^*) \times (-{d^2\vec h \over dt^2}) = (\vec R_Q^* - \vec R_{CM}^{\,*}) \times M{d^2\vec h \over dt^2}$. Therefore, the total fictitious force due to the translational acceleration of $O^*$ can be considered to act at the CM.

The torque from the other fictitious forces cannot be assumed to be equivalent to forces acting at the CM. This is also discussed in reference. [Diaz]

If $Q$ is chosen to be the CM, the torque from the fictitious force due to translational acceleration is zero and $$(22) \enspace {d\vec L_{CM}^{\,*} \over dt }= \sum_{i=1}^{k}\vec r_{iCM}^{\,*} \times (\vec F_i^{\,ext} + \vec F_i^{\,cent} + \vec F_i^{\,corio} + \vec F_i^{\,Euler})$$

For a rigid body with $O^*$ selected as a point within the body, the Coriolis force is zero. and $$(23) \enspace {d{\vec L_{CM\,rigid}^{\,*}} \over dt} = \sum_{i=1}^{k}\vec r_{iCM}^{\,*} \times (\vec F_i^{\,ext} + \vec F_i^{\,cent} + \vec F_i^{\,Euler}) $$ The Euler term is zero for constant $\vec \omega$.

The following addresses a possible area of confusion. The angular momentum of a rotating rigid body with respect to its CM in a non-inertial rotating frame- the body frame- in which the body is at rest, $\vec L_{CM}^*$ is zero since $\vec v_i^*$ is zero for every particle $i$. The angular momentum in the non-rotating space frame, call it $\vec H_{CM}$ with respect to the CM is not zero. $\vec L_{CM}^*$ and $\vec H_{CM}$ are not the same vectors.

With respect to the CM, $\vec H_B = {\bf I}\vec \omega$ where ${\bf I}\vec \omega$ is the moment of inertia in the inertial space frame, and $\vec \omega$ is the rotational angular velocity of the body in the inertial frame. $ {d\vec H_{CM} \over dt} = \vec N_{CM}$ where $\vec N_{CM}$ is the net torque with respect to the CM from the external forces in the inertial frame. [Kochmann]

For any (free) vector $\vec G$

$$\enspace (24) {d \vec G \over dt}|_{space} = {d \vec G \over dt}|_{body} + \vec \omega \times \vec G$$ [Goldstein] ${d \vec G \over dt}|_{space}$ is the derivative of $\vec G$ expressed in space coordinates. ${d \vec G \over dt}|_{body}$ is the derivative of $\vec G$ expressed in body coordinates. See my answer to The time derivatives of vectors in rotating frames on this exchange for a detailed discussion of relationship (24).

Using relationship (24) for a rigid body, the time derivative of the space frame angular momentum with respect to the CM can be expressed as $$(25) \vec N_{CM}= \bf I_{body} \dot {\vec \omega} + \omega \times {\bf I_{body}}\vec \omega$$ where $ {\bf I_{body}}$ is the constant inertial tensor in the body frame. [Kochmann]

The first term on the right hand side of relationship (25) is not the time derivative of the angular momentum in the non-inertial body frame where the body is at rest; it is the time derivative of the space frame angular momentum expressed using body frame coordinates. The time derivative of the angular momentum in the non-inertial body frame where the body is at rest is zero.

References

[Goldstein] Goldstein, Classical Mechanics

[Kochmann] https://ethz.ch/content/dam/ethz/special-interest/mavt/mechanical-systems/mm-dam/documents/Notes/Dynamics_LectureNotes.pdf.

[Symon] Symon, Mechanics

[Diaz] On the transformation of torques between the laboratory and center of mass reference frames (researchgate.net)