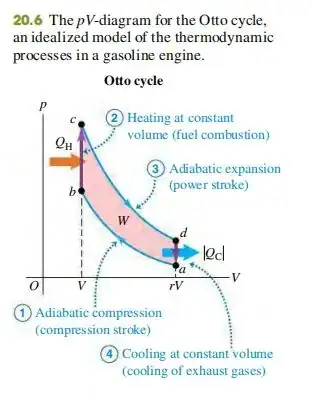
The diagram in the figure does not really represent the version of the Otto Cycle in an IC engine. It "simulates" this using what they call in the literature the "standard air Otto cycle." (Fundamentals of Engineering Thermodynamics, Moran et al; Introduction to Chemical Engineering Thermodynamics, Smith and Van Ness). In the IC version of the Otto cycle, there is no QH added in the first step, and energy is released to the gas by chemical reaction. In the standard air version of the Otto cycle, heat QH is added to an inert gas (air) to simulate the energy released by the chemical reaction.
The first law analysis of the IC version of the Otto cycle goes like this: In the first step, the system is adiabatic and isochoric, such that $$Q = W = \Delta U = 0$$In addition, for the ideal gas mixture that experiences the combustion reaction, the change in internal energy per unit mass is related to the internal energy change of reaction (per unit mass) by $$\Delta U=\Delta U_R+C_v\Delta T$$where $\Delta U_R$ is the internal energy change per unit mass in going from combustion reactants to combustion products at constant temperature. If we combine these two equations, we obtain: $$\Delta T=\frac{(-\Delta U_R)}{C_v}$$which, for an exothermic reaction is positive.
The first law analysis of the standard air version of the Otto cycle goes like this: In the first step, the system is isochoric, but receives heat $Q=Q_H$ from the surroundings, such that $$\Delta U=C_v\Delta T=Q_H$$So in this version of the process, neither the heat added nor the internal energy change is zero. From this equation, it follows that $$\Delta T=\frac{Q_H}{C_v}$$
Comparing these two versions of the Otto cycle, we see that the standard air version can be made to simulate the actual IC version of the cycle if we specifically choose $Q_H$ for the standard air version such that $$Q_H=-\Delta U_R$$