What is faster? Pure rolling or rolling with slipping?

Question

So we know that a ball will slide down an incline when there is no frictional force. Once you say there is static friction it causes a angular momentum which in turn causes a torque and makes the ball roll. Lets say the ball number one does pure rolling, where the static friction is large enough to keep it rolling pure all the way down. Now lets say ball 2 rolls as well, but slips some ways down the incline. What would reach the ground first? The ball rolling and slipping, or the ball purely rolling? If so, why?

Answer 1

The slip scenario caused a faster fall.

Less energy is converted into rotational kinetic energy if there is slipping, and thus (per energy conservation) more is converted into translational kinetic energy, which is a measure of the falling speed.

$$U=K_\mathrm{rot} +K_\mathrm{trans}.$$

Answer 2

For the ball (a solid sphere), with slipping, the acceleration of the Center of Mass (CM) of the body is $\ddot x_c = g(sin(\theta) - \mu cos(\theta))$ where $x_c$ is the acceleration of the CM, $\mu$ is the coefficient of friction, and $\theta$ is the angle of the incline. If $\mu$ exceeds ${2 \over 7} tan(\theta)$, the body rolls without slipping. $\ddot x_c$ is smallest when $\mu$ is this highest value, specifically $\ddot x_c = {5 \over 7} g sin(\theta)$. For any smaller $\mu$, $\ddot x_c$ will be higher.

The ball either slips or not depending on the values of $\mu$ and $\theta$; it cannot either slip, or roll without slipping, for the same conditions. For example, for a fixed $\theta$, the ball slips unless $\mu$ is sufficiently high.

So you cannot compare the two cases- slipping and rolling without slipping- for the same conditions; only one will occur. If you compare an incline with a $\mu$ sufficiently low to cause slipping to an incline with the same angle of incline but a different surface that has a $\mu$ sufficiently high to cause rolling, the acceleration for the slipping case is larger than for the rolling case and the ball will reach the bottom of the incline sooner for the slipping case.

Note: With no friction $\mu$ is zero and the acceleration is $\ddot x_c = gsin(\theta)$, the maximum value.

(See the text Analytical Mechanics by Fowles for a detailed derivation of the relationships used above.)

This response assumes a perfectly rigid body for which there are no heating effects. See Consistent Approach for Calculating Work By Friction for Rigid Body in Planar Motion.

In reality frictional heating occurs, and over a long distance would slow down the case with slipping, so my response is for slipping over a relatively short path down the incline. Since no body is perfectly rigid, as @Dast points out, if heating (increase in internal energy of the ball) is important the rolling case can be faster.

Additional response to questioner's comment about tape part way on the incline.

Acceleration decreases with increasing $\mu$, and $\mu$ is greater for pure rolling than for rolling with slipping. So if the tape has sufficient $\mu$ to allow pure rolling, and part of the incline has the tape and part has no tape to allow slipping, the ball will reach the bottom of the incline faster than if the incline has the tape all the way and only pure rolling occurs. Again, this assumes a perfectly rigid body (no heating).

Answer 3

For a reasonably long slope rolling is usually the faster option.

Lets say that we have a slope of a fixed height. We know once as the object has slid or rolled down the slope the potential energy of gravity is lost. This energy ends up split between three places: (1) The linear kinetic energy of the ball. (2) The rotational kinetic energy of the ball and (3) heat from friction.

Once the ball is rolling its surface that touches the slope doesn't rub against it at all. So no energy is lost to this friction. Small friction losses from the non-ideal real world (roughness and air) will remain, but we can probably neglect those and say that once the ball is rolling it doesn't loose energy over time to friction.

So if we compare a rolling ball to a sliding block. The ball has to pay an up-front energy bill to get rolling in the first place (investing in its rotational energy) so has less linear kinetic energy due to this. The block avoids this, but on the other hand it pays in kinetic energy the whole way down the slope as it rubs its way down. Its a one-time payment vs a continuous cost.

For a longer slope, or a higher coefficient of friction the one-time payment (rolling) has the advantage.

Answer 4

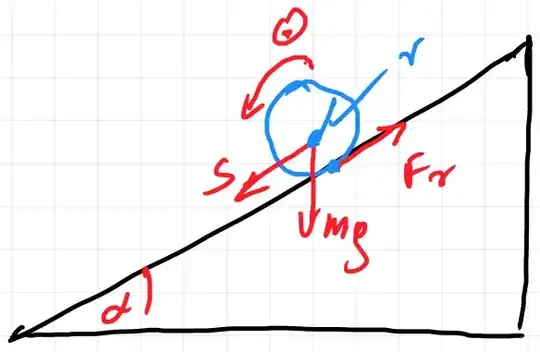
you have those two equations:

$$m\,\ddot s=m\,g\sin(\alpha)-F_r\\ I_\theta\,\ddot\theta=F_r\,r$$

in case of pure rolling is $~\ddot s=r\,\ddot\theta~$ and in case of partial rolling $~F_r=\mu\,m\,g\cos(\alpha)~$

pure rolling

$$\ddot s=\frac{m\,g\,r^2\,\sin(\alpha)}{m\,r^2+I_\theta} \quad \Rightarrow\\ s_1(t)=\frac{m\,g\,r^2\,\sin(\alpha)}{m\,r^2+I_\theta}\,t^2\quad (1)$$

partial rolling

$$\ddot s=g\,(\sin(\alpha)-\mu\,\cos(\alpha)) \quad \Rightarrow\\ s_2(t)=g\,(\sin(\alpha)-\mu\,\cos(\alpha))\,t^2\quad (2)$$

hence (with $~I_\theta=m\,r^2$)

$$\frac{\dot s_1}{\dot s_2}= \frac 12\,\frac{\sin(\alpha)}{\sin(\alpha)-\mu\,\cos(\alpha)}< 1$$

so partial rolling is faster then pure rolling