2

I have the following problem: (taken from Introduction to mechanics, Daniel Kleppner, problem 6.6)

A man of mass $M$ stands on a railroad car that is rounding an unbanked turn of radius $R$ at speed $v$. His center of mass is height $L$ above the car, and his feet are distance $d$ apart. The man is facing the direction of motion. How much weight is on each of his feet?

enter image description here

When I kook the torques with respect to the point between the man's feet I got $N_1=N_2=\frac{mg}{2}$ since the friction forces and gravity act in a parallel direction to the position vector, so they don't contribute to the torque equation. But this is of course wrong, since it dosen't take into a count the rotation of the cart on the railroad.
If I take the torques with respect to the center of mass it does take into a count the rotation of the cart on the railroad, since I get a contribution from the friction forces, which satisfy $f_1+f_2=\frac{mv^2}{R}$.
My question is: how come two different choises gives different results?
(I added the formal solutin, taken from Solutions Manual to accompany AN INTRODUCTION TO MECHANICS 2nd edition Version 1 November 2013)

enter image description here

Dvir Cohen
  • 35
  • interesting that N1 is an equal amount heavier than half his weight while N2 is an equal amount lighter. i use this stance to balance myself when standing on the subway train as it takes a sharp turn. – mcodesmart Dec 25 '21 at 18:49
  • @mcodesmart Since the total vertical force from the floor must equal his weight, how else could it be? – DJohnM Dec 25 '21 at 20:57
  • The total force is indeed equal to his weight. Add n1 and n2 and the terms cancel out. – mcodesmart Dec 26 '21 at 03:13

2 Answers2

1

In general, the angular momentum of a system of particles about a reference point is equal to the angular momentum of the center of mass (CM) about the point plus the angular momentum of the motion about the CM. Using the CM as the reference point, the angular momentum of the CM is always zero so the angular momentum of the system is the angular momentum about the CM.

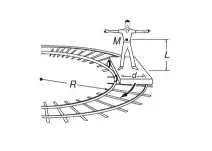
In your case, the angular momentum of the person about the CM is zero assuming the person is not swaying, but the CM of the person has linear acceleration inward due to the centripetal force from friction. For a body that is accelerating, if you take the reference point at the CM it is always true that ${d \vec L_{CM} \over dt} = \vec \tau_{CM}$, where $\vec L_{CM}$ is the angular momentum and $\vec \tau_{CM}$ is the net external torque about the CM; basic physics texts state this, which is true, without proof. It is not true in general that ${d \vec L_Q \over dt} = \vec \tau_Q$ for any reference point Q other than the CM if the body is accelerating; for proof see a physics mechanics text such as Mechanics by Symon, or Classical Mechanics by Goldstein. Since the angular momentum of the person about the CM is zero, the total angular momentum with respect to the CM is zero; therefore, the sum of the torques about the CM is zero as indicated in the solution, even though the CM is accelerating inward.

You can use a reference point $Q$ that is not the CM, but there is an extra term for torque in this case. Specifically, ${d \vec L_Q \over dt} = \vec \tau_Q -M(\vec R - {\vec r_Q}) \times \ddot {\vec r_Q}$ where $M$ is the mass, $\vec R$ is the position of the CM with respect to the origin of your inertial system, and $\vec r_Q$ is the position of point Q with respect to the origin of your inertial system. In general this can be complicated to evaluate, but for your case: $-M(\vec R - {\vec r_Q})$ is a vector downwards with magnitude $Mh$ where $h$ is the distance from the point Q (the point between the feet) and the CM, $\ddot {\vec r_Q}$ is a vector inwards with magnitude ${v^2 \over R}$. Also, $\vec L_Q$ is zero since there is no sway of the person about the point Q between the feet. Taking the vector directions into account we have: $0 = (N_1 - N_2){d \over 2} - {Mhv^2 \over R}$, or $(N_1 - N_2){d \over 2} = {Mhv^2 \over R}$. Note: I use $h$ instead of $L$ for the distance from $Q$ to the CM because I reserve $L$ to mean angular momentum.

You obtain the same answer for the normal forces using the CM or the point between the feet as your reference point, but in general you should always use the CM as the reference point for an accelerating body, because the evaluation using another point can be very complex.

Also see the question About $\frac{d L}{d t}=\tau$ in a rotating center of mass frame on this exchange. The answer @Kashmiri provides is essentially the same as I provide here.

John Darby
  • 9,351
  • I can't understand why $\frac{dL}{dt}$ applies only if the axis is at the COM (in an accelerating system), does $\frac{dP}{dt}=F$ no longer apply? And if it doesn't, why taking the axis throug the COM works? – Dvir Cohen Dec 25 '21 at 19:13
  • I updated my answer. dP/dt = F always holds for the motion of the COM in an inertial (non-accelerating) reference frame. In a non-inertial frame, you have to consider the fictitious forces. – John Darby Dec 25 '21 at 23:00
0

Your first equation contains no torques and is not true. For torques about a point between his feet: $({N_2} – {N_1})(d/2)$ = dL/dt = (d/dt)(mvh) = mh($v^2$)/R where I'm taking (L) as the angular momentum about the reference point and h as the height of the center of mass. (This is consistent with the book solution.)

R.W. Bird
  • 12,139