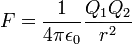To what extent are quantities fundamental?

Question

Arguably the most well-known and used system of units is the SI-system. It assigns seven units to seven ‘fundamental’ quantities (or dimensions). However, there are other possible options, such as Gaussian units or Planck units. Until recently, I thought that these different systems differed only in scale, e.g. inches and metres are different units, but they both measure length. Recently though, I discovered that it is not simply a matter of scale. In the Gaussian system for example, charge has dimensions of $[mass]^{1/2} [length]^{3/2} [time]^{−1}$, whereas in the SI-system it has dimensions of $[current] [time]$. Also, I have always found it a bit strange that mass and energy have different units even though they are equivalent, but I find it hard to grasp that a quantity can be ‘fundamental’ in one system, and not in an other system.

Does this mean that all ‘fundamental’ quantities are in fact arbitrary? Would it be possible to declare a derived SI-unit fundamental, and build a consistent system with more base units? What is the physical meaning of this?

Answer 1

The key difference is the $ \frac{1}{4\pi\epsilon_0} $, with $ \epsilon_0 $ in the SI formulation of charge, being vaccuum permittivity with units $ (charge)^2(time)^2 (mass)^{−1}(length)^{−3} $. This satisfies the unit cancellation, and in the SI system makes the electric constant $ \mu_0 $ and $ \epsilon_0 $ now derived units. (See Vacuum Permittivity or SI Unit Redefinition)

For example, Coulomb's law in Gaussian units appears simple:

where F is the repulsive force between two electrical charges, Q1 and Q2 are the two charges in question, and r is the distance separating them. If Q1 and Q2 are expressed in statC and r in cm, then F will come out expressed in dyne. By contrast, the same law in SI units is:

where $ \epsilon_0 $ is the vacuum permitivity, a quantity with dimension, namely (charge)2 (time)2 (mass)−1 (length)−3. Without $ \epsilon_0 $ , the two sides could not have consistent dimensions in SI, and in fact the quantity $ \epsilon_0 $ does not even exist in Gaussian units. This is an example of how some dimensional physical constants can be eliminated from the expressions of physical law simply by the judicious choice of units. In SI, $ \frac{1}{\epsilon_0} $, converts or scales flux density, D, to electric field, E (the latter has dimension of force per charge), while in rationalized Gaussian units, flux density is the very same as electric field in free space, not just a scaled copy. Since the unit of charge is built out of mechanical units (mass, length, time), the relation between mechanical units and electromagnetic phenomena is clearer in Gaussian units than in SI. In particular, in Gaussian units, the speed of light $c$ shows up directly in electromagnetic formulas like Maxwell's equations (see below), whereas in SI it only shows up implicitly via the relation .

- Wikipedia: Gaussian Units

Yes, I would argue that 'fundamental quantities' are indeed arbitrary, as are many of our choices, such as base-10 number systems. This is illustrated well on the Golden Record we put on voyager spacecraft, for decoding by other intelligent life; we show how fast to spin the record by relating time units in the fundamental transition of the hydrogen atom:

I'd then add that we have tried to make them as least-arbitrary (to us) as possible, but there's no reason that some other intellegence would have different 'fundamental unit' definitions and scalings, or whatever 'arbitrary' units they came up with. We could use $ (time)^{-1} $ or 'period' as our fundamental timing unit, and change all the other derived units to follow, if we wanted.

Answer 2

What you call "fundamental quantities" are correctly called "base quantities". Base quantities are chosen by convention, not by fundamental reasons. Yes, you could choose a different set of quantities and declare them as base quantities.

See: International vocabulary of metrology — Basic and general concepts and associated terms (VIM).

Answer 3

The Si - Units are just a definition which are related by euqations. Take for example the speed of light $c \approx 3\cdot 10^8\frac{m}{s}$. Now what does $\frac{m}{s}$ mean? You can take it as a parameter that is connected to other units by equations like the famous $E = m c^2$. Since only the equation is important and you have to define your unit somehow you could also say that $c = 1$.

What I did here is nothing else than to set $$\frac m s = \frac 1 {3\cdot 10^8}$$ You can always do this for the first unit you change, but you have to be careful if you change a second unit as those units may be connected by an equation.

Take again $E = mc^2 = m$ where I have set $c = 1$. Now there is one more independent unit: Either mass or energy which you also can choose as you like. As you can see there is an infinite number of possibilities to choose the units, but as people have to communicate it is a very good advice to keep on the standard units in the different fields of science.

An important note is the following: We have set $c = 1$ this means, that length has the same unit as time. Take as an example a star $\Delta x = 100 c \cdot s$ away. Here $c \cdot s$ are light seconds. As we have set $c = 1$ you can clearly see that $\Delta x = 100 s$ which is not very intuitive but you have to keep in mind that $c = 1$ and with this you can always change from meters to seconds with $s = 3\cdot 10^8 m$ in this system.

Answer 4

One should remember that 'length', 'mass' and 'capacity' are the base standards of the commercial systems, where 'capacity' is volume measured by bulk comparison, eg pouring or weighing.

NASA, for example, used the inch-pound-second system, since these are the base units defined in US legislation. The unit of 'slinch' (ie 386 lb = ips slug), has been observed, along with a measure of a slinch-mole (written as (lb-g-s^2/in)-mole ).

The scientific systems are essentially selected from length and mass, along with a time unit. There really is no need to follow the legal standard, except you might run into legal problems down the track.

The number of base units depends on the number of free variables you would have in a system. The size of the units do not change with dimension, this is because the dimension is relative to a body of equations, which define X quantities in (X-B) equations. The B remaining quantities are defined in the preamble.

For example, the mole was a derived unit, essentially "mass/daltons". The daltons were found from the chemical tables, and divided into mass, to give mass-mole. This is a derived unit, with dimensions M.

In SI, the coherent unit is not 'dalton' but 'kilodalton', so the unit mole is actually 'kilogram / kilodalton', but the tables still show the weights in daltons. So there is an additional constant in the CODATA tables that gives kilodaltons. (ie 1 kg/dalton = 1000 moles)

Were one to construct base units that actually meant something to science, then the choice would be something like density, velocity, time. Density is something that really is constant from atoms to stars. Velocity is consistant with the thermal state of things. Size is then dependent on the appropriate power of time. In SI, replacing time with 10^-9 seconds, would pretty much eliminate all of the exponents in the CODATA atomic values, and with t=10^-12, v=10^3 (ie thermal velocities), nearly all exponents disappear.

The correct approach to dimensions is to simply regard them as algebraic blobs, which can be multiplied, divided etc. Note that any given system does not have a full set of dimensions, and a full set would make the mathematics unwealdy. None the same, Leo Young in 1961, showed a set of equations, to which the cgs-gaussian, and SI were both coherent to, by supposing two additional base units assumed different values in the different systems.

Answer 5

One must remember that SI is defined for ease of use and human familiarity. Natural unit systems have two problems in this regard: it's hard to keep track of the units and therefore avoid trivial mistakes like calling a length a volume or a time a frequency, and the constants involved are either impractically huge or impractically tiny at the human scale, making the units impractically sized as well. This is why SI defines the units it does.

Length and time are kept distinct because the conversion factor between them (the speed of light) is ridiculously huge. A light-second is about three hundred thousand kilometers, which is too big. And while a light-nanosecond is about a foot, a nanosecond itself is too small. As a result, we give the speed of light a unit (meters per second) and a numerical value that allows us to switch easily between the predefined values of second and meter, so we can then throw those definitions away and use the new, lightspeed based one.

And if you think length and time have it bad, remember that mass and energy have the same conversion factor, but squared. A square-light-kilogram is about ninety thousand million million joules, an amount of energy we will never attain except possibly in our wildest fantasies. And trying to go the other way leaves us with a mass unit even smaller than a nanosecond. So instead of using the speed of light to convert between mass and energy, we use the ratio between a meter and a second.

Of course, energy and time are related by Planck's constant, or the "action quantum" (I just made that term up), but it is ridiculously tiny - even more than lightspeed is ridiculously huge. So we do the same thing, we give it a unit (joule second) and a numerical value that allows us to switch easily between the predefined values of joule and second, so we can throw those definitions away and use the new, Planck based one.
Except that it's actually much easier for us to directly measure mass than energy, so we measure a kilogram, multiply it by a meter-per-second squared (not be confused with meter per second-squared) and call that a joule, then throw away the predefined value of a kilogram to use the new, Planck based one (which we finally did in 2019).

Then there's amperes. The choice to define an electric unit rather than just derive it from $LTM$ (length, time, mass) was because there were multiple ways to do it, unlike, say, energy, which is always $[M][L]^2[T]^{-2}$. Sure, the Gaussian (electrostatic) definition of charge was $[M]^{1/2}[L]^{3/2}[T]^{−1}$, but the electromagnetic definition of charge was $[M]^{1/2}[L]^{1/2}$.

The discrepancy is caused by which relation you consider fundamental. ESU (electrostatic units) starts from Coulomb's law; EMU (electromagnetic units) starts from Ampere's law. These two methods create units of charge that differ by a factor of lightspeed, hence the different units. SI went with Ampere's law since it was easier to measure, hence the choice of ampere over coulomb, but has since decided to count electrons per second, deciding that the fundamental unit is the quantum of charge. This, by the way, is why you don't hear anything about "units of color charge" or "units of flavor charge"; the counts of charge quanta are treated as unitless counts, sidestepping the whole issue.

Similarly, you may have heard that "temperature is just energy". It's not, it's energy per unit entropy. It's just that entropy is fundamentally a description of information, so it can be reduced to a unitless count of "bits" or "degrees of freedom". Likewise, amount of substance is just counting particles; the mole is simply a convenient number to switch between the realm of particles and the realm of substances. As for luminous intensity, the very concept depends on the sensitivity of the human eye; candelas would not be missed outside of photometry, and indeed aren't.