Are constraint forces infinite?

Question

A lot of authors claim that mechanical constraints are idealizations obtained by allowing enforcing forces to be infinite. But I either disagree or don't know what they mean. The only case where I would find it to be true is these forces were impulsive, i.e., the velocity would change abruptly through the means of Dirac delta impulses.

On the other hand, all the text books present a theory where the constraint forces are always bounded and smooth (either as Lagrange multipliers or the limit of a very strong potential). This makes me think they can never be infinite and there is no reason for them being infinite. The only possibility I see is that only the stiffness of the force potential goes to infinity (while also assuming that the constraint violations/oscillations are small).

Which view is right? And also, would there be any damping involved?

Qmechanic · Answer 1 · 2022-01-27T20:16:45.487

9

OP already seems to have thought long and hard about this and makes good points. In this answer we will review the argument for why constraint forces could be infinite.

We will assume that OP talks about holonomic$^1$ constraints. To be concrete, let the constraint be that some generalized coordinate vanishes $$q~\approx~0.$$ We can implement the constraint

ideally via a Lagrange multiplier term$^2$
$$L_1~=~L_0 +\lambda q,\tag{1}$$ where the constraint force can be identified with the Lagrange multiplier $\lambda$;
or pragmatically via a stiff spring potential $$L_2~=~L_0 -\frac{k}{2} q^2,\tag{2}$$ where the spring constant $k$ is very large.

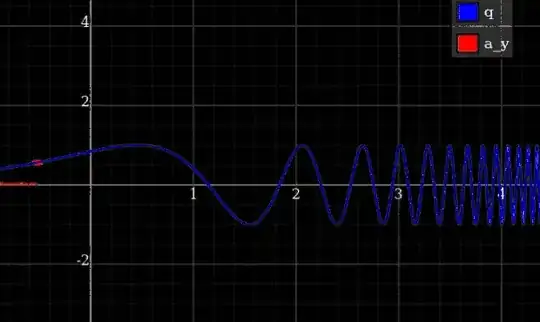
If $E$ denotes a characteristic energy available to the system, it is reasonable to expect $$\frac{k}{2} q^2~\lesssim~ E,$$ or $$|q|~\lesssim~{\cal O}(k^{-1/2}).$$ Hence the spring force $$ |F|~=~|-kq|~\lesssim~{\cal O}(k^{1/2})~\to~\infty\quad{\rm for}\quad k~\to~\infty.$$ In other words, the spring force $F$ could be very large, and unbounded from above as $k\to\infty$. Of course, it might not be large at all the time. E.g. there could be an oscillatory pattern.

In particular, if one identifies the spring force $F$ in model 2 with the constraint force $\lambda$ in model 1, one can argue that the (absolute value of) the latter could be very large, cf. OP's title question.

We can unify model 1 & 2 via the Lagrangian $$L_3~=~L_0 +\frac{\lambda^2}{2k} +\lambda q.\tag{3}$$ The EOM for $\lambda$ is $$\lambda~\approx~ -kq.$$
- On one hand $$ \lim_{k\to\infty} L_3~=~L_1.$$
- On the other hand, for finite $k>0$, if we integrate out/eliminate $\lambda$ from $L_3$ via its EOM, we exactly get $L_2$.

--

$^1$ Semi-holonomic constraints are quite subtle, cf. e.g. this Phys.SE post.

$^2$ The Lagrangian $L_0$ could in principle contain many degrees of freedom, i.e. depend on many generalized coordinates. We will assume that the system has at least 1 more coordinate than $q$, so that the system is non-trivial.

edited Jan 27 '22 at 20:16

answered Jan 25 '22 at 15:03

Qmechanic

201,751

If you have $L_0 = T-V$, then I would write a characteristic energy as $E\sim H= T+V$. To me it looks like you'd need $kq^2/2>>E$, otherwise the amount of energy in the system would excite the harmonic oscillator and constraint wouldn't be enforced. How do you conclude that $kq^2/2 \le E$? – Jojo Jan 25 '22 at 21:43
There may be oscillations, the point is to limit its amplitude. – Qmechanic Jan 25 '22 at 22:20
Hi @Joe, I recorded you edits so that we have them, but I'm still not convinced that your improved argument is necessary. – Qmechanic Jan 25 '22 at 22:39
Well, I think you're missing the step of splitting the energy into the constrained and constraint part, but it is your answer so fair enough. It's a nice argument either way, I've not seen it before. – Jojo Jan 25 '22 at 22:45
2

Here's what I'm trying to say; importantly there are two characteristic energy scales. $E_0$ characterises motion within the constraint surface $q=0$, and $E$ characterises movement within the whole phase space. We need $E_0<<E$ for $kq^2/2$ to act as a constraint. I had to work out what you meant when I read your answer because it doesn't differentiate between the two scales, so '$E$ denotes a characteristic energy' was not clear to me. – Jojo Jan 25 '22 at 23:10
@Qmechanic Thanks for the answer. Isn't the solution for $kq^2/2$ always a harmonic oscillator? Even if $k$ goes to infinity wouldn't the oscillations stay bounded for a finite energy $E$? I figure the amplitude of the oscillations which you're trying to estimate the order of only depends on the initial conditions and how far away they are from the constraint manifold, and ultimately the total energy $E$ in the embedding phase space. So, maybe I'm missing something, but I don't think it's reasonable to assume $q \sim k^{1/2}$. – zetzar Jan 27 '22 at 18:36
My main problem with this is that although it seems that the gradient of the potential function seems to go to infinity (as for a "wall"), the acceleration does not (as a periodic trigonometric function, even if the frequency tends to infinity). Also, when you're multiplying a very large $k$ with $q$ which can be zero you get some kind of very steep "well" for when the constraint is satisfied. So, the potential is not everywhere infinite. Somehow, because of $m\ddot = -kq$ I would argue the force stays finite. – zetzar Jan 27 '22 at 18:52
Well, it's a matter of limits. I updated the answer. – Qmechanic Jan 27 '22 at 20:15
I'm sorry, but I'm still not seeing it. I was wrong about the accelerations and the velocities, they do go to infinity with $k$, but at least the oscillations stay bounded. But I see it as more of alternation of positive and negative delta Dirac spikes, such that the average line of equilibrium still makes sense. Otherwise I don't see how $L_3$ tends to $L_1$ without $kq$ having some kind of convergence towards $\lambda$. And $\lambda$ is a finite value coming from the algebraic condition and probably the average of the oscillation force. – zetzar Jan 28 '22 at 17:41
What is EOM? (it could not be equation of motion, could it?) 2. And is there a special name for the 3rd Lagrangian? I would like to search it up online. Thanks!

Cheng

Nov 05 '22 at 00:23

EOM=equation of motion.

– Qmechanic Nov 05 '22 at 11:41

score 8 · Answer 2 · answered Jan 25 '22 at 14:19

I think there is no single answer to this question; it depends on circumstances. If you have a three-dimensional region of space, with a sphere sitting in it, for example, then you might have a particle whose motion is constrained to lie on the surface of the sphere. In setting up Lagrangian mechanics for this case, you don't have to invoke any notion of force; you can deal with it as a constraint. But if you then ask what kind of force would result in the same motion, then it is a 'hard wall' type of force, which rises to infinity as soon as the particle position moves away from the sphere's surface.

One could also notice that we commonly do mechanics in a three-dimensional space, and you could say that the particles were 'constrained' to stay in the 3D space and not wander off into some 4th dimension. In this case one is concerned with a physical problem in which there simply is not any 4th spatial dimension. So we would not ordinarily call that a constraint, but mathematically speaking it has the same effect as a constraint.

Overall I think the answer is that some cases where we invoke a constraint, that is a convenient way to handle what really is the result of a force, and other cases are not.

My issue with how this forces rises to infinity as soon as you move away from the constraint manifold. Because the constraint force as given by the Lagrange multipliers does not go to infinity: it is finite and sufficient to keep the motion on the sub-manifold. I have no problem with constraints as idealizations, I like them just as much as mathematical constructs, although this article kind of ruined my hopes of them being something too fundamental: https://aapt.scitation.org/doi/abs/10.1119/1.13647 — zetzar, Jan 28 '22 at 17:33
@zetzar what do you mean by "of them being something too fundamental"? — Cheng, Nov 05 '22 at 03:17
@Cheng Fundamental as in fundamental forces. Usually constraints are the result of very stiff forces, like inter-molecular forces. There was a time when I was day-dreaming that constraints are actually more fundamental in nature, that they exist before forces, and not the result thereof. Like moving on a circle in 2D space. Basically, that Lagrangian mechanics on manifolds is not an idealization, but that's how nature really works at some levels. But it's probably wrong and I haven't though about it in a long time now. — zetzar, Nov 07 '22 at 09:44

score 3 · Answer 3 · answered Jan 26 '22 at 14:59

3

In practice you're of course right, however allowing for infinite forces is the easiest way to handwave exact fulfillment of the constraints.

As argued in Qmechanics answer, in practice the energy is limited, then the stiffer you make the spring constant the less max deviation you get from the exact constraints. The idea is that you can then compute the dynamics for any finite $k$, obtain the limit $k\to\infty$, and there the deviations will tend to zero but the maximum forces still stay finite. In other words, you could replace the $\tfrac{k}2q^2$ potential with a capped version, $\max\{E, \tfrac{k}2q^2\}$ or something smooth like $E\cdot\tanh(\tfrac{k}{2E}q^2)$. That is actually not sufficient to guarantee the forces will stay bounded though.

An example where you do get infinite forces is a particle constrained to a trail $$ q\in \bigl\{(x,y) : y = \sin(\exp(x))\bigr\} $$ with no other forces. As the particle travels rightwards, it will pass every $y$-maximum with the same $x$-velocity due to conservation of kinetic energy. But there it has a $y$-acceleration $\propto -\exp(x)$, which grows without bounds.

(Real-world application: a high speed train rolling into a tight corner without braking first won't be saved by the fact that the rails are almost perfect constraints.)

To get a bound on the maximum force, what you need is a bound on the curvature of the constraint manifold, in addition to a bound on the energy.

answered Jan 26 '22 at 14:59

leftaroundabout

14,903

That's a nice point that the curvature of the constraint plays a role. And that's actually contained in the Lagrangian formalism: the Lagrange multipliers will always oppose the inertial forces. But I'd say that's an edge case. I was talking about well-behaved constraints like a circle. – zetzar Jan 27 '22 at 18:41
I'm not sure I follow your energy argument, but I think we agree that for a maximum and finite total energy $E$ the forces and displacements will stay finite too. The forces may look like spikes, but I'm not sure they qualify as delta Dirac functions, and that would be the closest to an infinite force I can imagine. – zetzar Jan 27 '22 at 18:44
They approach Dirac spikes, yes. It's like a perfectly stiff but elastic marble bouncing on a hard stone surface. A somewhat less contrived example that does this with a holonomic constraint is a round-bottom channel and gravity that gets more and more pointy V-shaped. But you could even have sustained infinite forces, with some funnel that gets narrower and narrower. Sure you can call all these “edge cases”, but... well, literally. And edges and hard surfaces are by no means a silly theoretical thought experiment, but actually the best way to model many engineering problems. – leftaroundabout Jan 27 '22 at 18:59
From where did you get that simulation? Do you have any guides to making such simulations? Thanks! – Cheng Nov 05 '22 at 00:24
@Cheng I don't seem to have kept the source code for that particular simulation. It is pretty easy, because the speed is constant, so you just need to parameterize the curve by path length and then uniformly move along that path. I don't think the parameterization can be done analytically, but numerically it just amounts to going along $y(x)$ iteratively with a $\Delta x$ such that $\sqrt{(\Delta x)^2 + (y(x) - y(x+\Delta x))^2} = h$, which can be Taylor-approximated as $\Delta x = \frac{h}{\sqrt{1 + (y'(x))^2}}$. That would be like 5 lines of Haskell. – leftaroundabout Nov 05 '22 at 10:14
...This discretized form isn't great for computing the acceleration though, not sure if I did it that way. – leftaroundabout Nov 05 '22 at 10:19

score 2 · Answer 4 · answered Jan 26 '22 at 14:19

When you simplify your coordinate system with mechanical constraints, you are assuming that:

The system will stay on the constrained path; and
There will be no energy stored in the constraints.

As a real mechanical constraint becomes stiffer, i.e., the magnitude of its restoring force as a function of deviation increases, it approaches this ideal more closely, in that you must apply increasing force to achieve a certain deviation or to store a certain amount of energy.

In the limit, the restoring force approaches infinity and the assumptions hold as long as the forces against the constraints are finite.

This is close to what @Qmechcanic said, except that the key idea is that no finite force could store any energy in the constraints, so there can be no oscillations against the constraints or anything like that.

score 1 · Answer 5 · answered Jan 26 '22 at 17:14

This is physics, so the question should boil down to what you'd measure in an experiment. What would you see if you built a constrained mechanism and placed a load cell at the point where the constraining force is applied? The answers above give you theoretical approaches, noting that a load cell is actually a very stiff spring with a very sensitive strain gauge. If you're doing real physics and not textbook problems, you should build the mechanism and use it to test your results.

Or perhaps, the question should be whether the idealization will get you in trouble, leading to unrealistic results. This, of course, affects all applications of mathematical infinity in physics. In general, it's a difficult question. Textbooks tend to map the paths through the minefield that you'll need to solve their problems, but at the end you don't know where the mines actually are.

Are constraint forces infinite?

5 Answers5