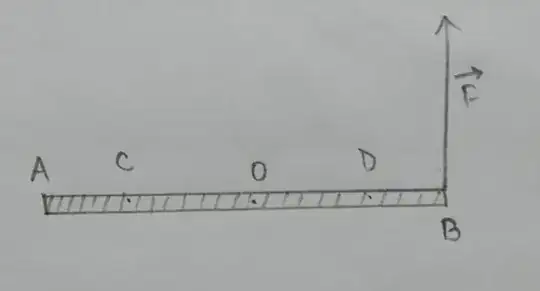
Here, $O$ is the center of mass of the uniform and rigid bar. $O$ is not affixed. In fact, none of the points on the bar are affixed. Now, a force $\vec{F}$ acts at $B$.
There's no doubt that the stick will start rotating as the force has not been applied at the center of mass. Now, the question is, about which axis will the stick start rotating?
In this situation, the torque can be calculated in an infinite number of ways. We can calculate the torque about $A, C, O, D, B,...$ and so on. Which is the correct axis to take?
For example, torque about $A$,
$$\tau_A=F\cdot AB$$
Again, torque about $C,O,D$ and $B$,
$$\tau_C=F\cdot CB$$
$$\tau_O=F\cdot OB$$
$$\tau_D=F\cdot DB$$
$$\tau_B=F\cdot 0\tag{1}$$
My understanding:
I think that in this case taking the torque about any of the axes is correct. Taking the torque about any of the axes will reflect the physical scenario accurately. For example, we can understand from common sense that there will be no rotation about $B$, and this is what we found in $(1)$.
In other words, the rotation that will be produced due to the torque about $A\ (F\cdot AB)$ is the exact same rotation that will be produced due to the torque about $C\ (F\cdot CB)$ or $O$, or $D$ or $B$. Taking the torque about the different points are different ways of expressing the same physical scenario.
Question:
- Is my understanding correct?