Say we have a cylinder rolling without slipping on a horizontal plane:
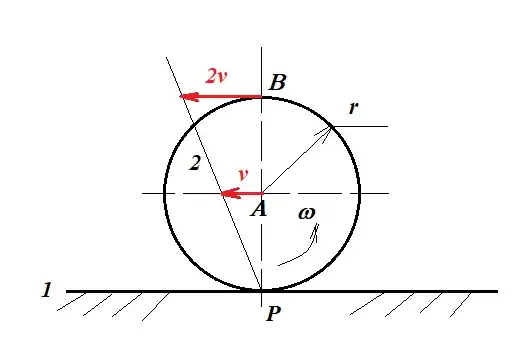
Now, the instantaneous centre of rotation is P, so we can use $ v_A=\omega \ r_{AP}$ to find the linear velocity of the centre of mass, and calculate: $$\mathrm{KE}_{\mathrm{translational}} = 1/2 mv_A^2$$
However, my question is to do with computing the rotational KE. If P is the instantaneous centre and the cylinder is rotating about P, then why do we not use moment of inertia about P in the equation for rotational KE?
Why is it $\mathrm{KE}_{\mathrm{rotational}} =1/2I_A \omega^2$ and not $1/2 I_P \omega^2$?
The moment of inertia in rotational KE is defined to be the moment of inertia about the axis of rotation. Now I can see, of course, that the cylinder's axis of rotation over the course of its motion is A. However, isn't the bottom of the cylinder in contact with the ground always an axis of rotation too? What am I missing here?