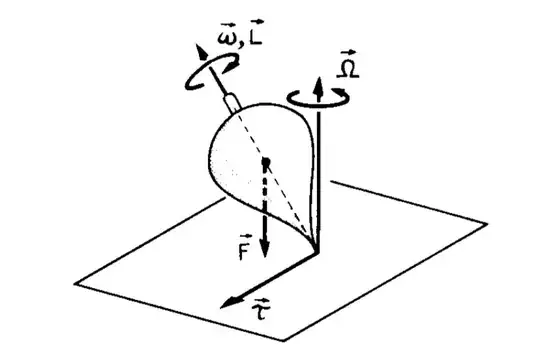
Confusion about the Spinning Top

Question

Consider the following symmetric spinning top with a fixed point on the horizontal surface.

I have two questions concerning its motion:

let $\underline{\Omega}$ denote the precession angular velocity, that is, the angular velocity of the reference frame of the spinning top with respect to the inertial reference frame of the laboratory, then, applying the second cardinal equation and Poisson theorem yields: $$ \underline{\Omega} \times \underline{P_c} = \underline{r_c} \times M\underline{g} $$ where $\underline{P_c}$ represents the angular momentum with respect to the center of mass and $\underline{r_c}$ represents the position of the center of mass with respect to the fixed point; my question is how do we find out that $\underline{\Omega}$ must be directed vertically as in the above figure, since actually infinitely many vectors satisfy the previous relation?
assuming we have demonstrated that the spinning top follows a precession around the vertical axis, then, in that case, the center of mass is also rotating around such axis, therefore it should have a centripetal acceleration but what is the force responsible for it? (I thought about friction on the fixed point but the fact is that in any reference I have found friction is never talked about)

As always, any comment on answer is highly appreciated! Also, let me know if I can explain myself in a clearer way!

There is a discussion here on physicsSE (submitted in 2012 by me) of gyroscopic precession. That discussion capitalizes on symmetry to make the physics taking place transparent. The discussion is illustrated with 3D renderings of a gyroscope wheel. It is demonstrated that the combination of the gyro wheel spinning and swiveling gives rise to a pitching effect. This pitching effect provides the centripetal effect you are asking about. — Cleonis, Jul 03 '22 at 07:56
About the pitching effect mentioned in my previous comment: when the ground contact is frictionless the pitching motion will be around the center of mass of the gyroscope. When the ground contact is a fixed point then the pitching motion will be around the ground contact point. — Cleonis, Jul 03 '22 at 08:05

score 2 · Answer 1 · answered Jul 19 '22 at 04:28

Let's start with your first question. You are right that an infinite number of vectors satisfy this equation, and in fact you could think about the top as instantaneously rotating about them (like in rolling without slipping). However, once we apply the condition that our torque must stay $r_c \times Mg$ through the whole rotation we see that the only case that physically keeps this condition is going to be rotating about the z axis as every other rotation involves some change in z value which would change our gravitational force which we assume is constant when we look at precession so we must have a constant z value and thus $\Omega$ points in the $\hat{z}$ direction (if you are interested in the case where we look at a changing z Taylor Classical Mechanics has a good section on nutation). $$$$ For your second question we can look at it in two ways. The first is from a physics problem perspective which just lets us say that there is some constraint force acting at that point to keep the tops tip from moving. However, we can also look at this from the point of view of what actually happens when you spin a top, and the answer to this is its going to be friction keeping the top tip in place (although it might move depending on the top and what you spin it on).

score 1 · Answer 2 · answered Jul 19 '22 at 05:53

The answers are:

there is no single vertical $\Omega$
it's usually friction, just as you mentioned

To see this, let's look at some tops.

This one shows that tops don't have pure precession with a single angular frequency $\Omega.$ Instead, they bounce around some, a motion called nutation.

(The gif doesn't really show a "top", but the nutation is easier to see in this setup than in a normal top.)

Here's a more typical top:

The contact point slides around as the top spins. The center of mass of this top doesn't accelerate nearly as much as it would if the contact point were fixed.

The contact point of a top is only fixed if there is a force preventing it from sliding. That would usually be friction, as you pointed out, but you could also place the top in a divot, for example.

It is possible to set up a top so that the nutation is negligible, and so that the contact point doesn't slide noticeably. That makes modeling the top easier. I would guess that whatever sources you read made these assumptions. In more detailed models, the dynamics are quite complicated, especially due to friction.

Video sources:

nutation: https://www.youtube.com/watch?v=_v_GU1P9L2g&t=172s

sliding top: https://www.youtube.com/watch?v=uf-UFu-lACY&t=30s

score 0 · Answer 3 · answered Jul 04 '22 at 00:22

0

I think your equation $\Omega\wedge P_c=r_c\wedge Mg$ is not correct. The l.h.s. should be the derivative of the total angular momentum w.r.t. to point of contact with the floor, not w.r.t. the center of mass.

answered Jul 04 '22 at 00:22

facenian

416

Yeah, you are right, I should mention however that the normal reaction of the plane is equal and opposite to the weight, hence one can derive such equation with respect to the center of mass and it has the same form – Matteo Menghini Jul 04 '22 at 06:34
I was talking about the total angular momentum w.r.t. to point of contact with the floor. Now I see your equation is w.r.t. to the center of mass frame. Yes, in that case, we have to use the reaction of the floor. Notice that there is also a horizontal component of the reaction. – facenian Jul 04 '22 at 10:53
By the way, the horizontal component is the response to your second question. To move the way you are considering, the point of contact has to be bound to a fixed point on the floor. – facenian Jul 04 '22 at 12:45
Thank you for pointing that out but how to prove it rigorously? – Matteo Menghini Jul 04 '22 at 14:05
1

Good question. I wish someone could enlighten us. – facenian Jul 04 '22 at 16:51

Confusion about the Spinning Top

3 Answers3