4

I am trying to understand an interesting effect I observed while playing with my kids' toys (video). The energy in this system seems to slosh back and forth between the trough and the ball, with the ball periodically almost coming to rest. I'm hoping to get a better understanding by developing the dynamics equations describing the system.

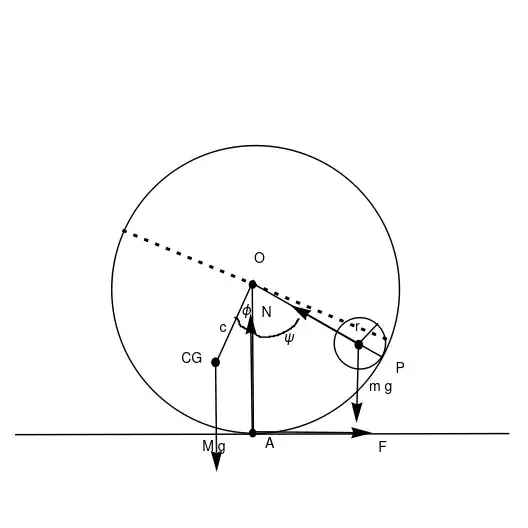
The problem can be reduced to two dimensions since the center of mass of the ball and the trough move in the same plane (assuming the ball starts in the center of the trough).

2D schematic of the ball inside the trough

The equations for the motion of the trough alone are relatively easy to compute (equations). I extended the Lagrangian approach to include the ball. This is also relatively straightforward since potential and kinetic energies are just the sums of the corresponding energies for the ball and the trough.

$$ T_t=\frac 12\,{\dot\varphi }^{2} \left( M{R}^{2}-2\,M\,R\,c\cos \left( \varphi \right) +M{c}^{2}+I_{{C}} \right) $$ $$ U_t=M\,g \left( R-c\cos \left( \varphi \right) \right) $$ where $\phi$ is the angle between the vertical and radius through the center of mass, $M$ is the mass of the trough, $R$ is its radius, $c$ is the distance of the center of mass from the cylinder's (encompassing the trough) axis of symmetry and $I_C$ is the moment of inertia of the trough about its center of gravity.

For the ball I'm getting $$ T_b=\frac 12\, Ib \left(\frac{\dot{\psi} R}{2 \pi r}\right)^2+\frac{1}{2} m \left((\sin (\phi+\psi) (\dot{\phi} R+\dot{\psi} (R-r)))^2+(\cos (\phi+\psi) (\dot{\phi} R+\dot{\psi} (R-r))-\dot{\phi} R)^2\right) $$ $$ U_b=m\, g\, R (1 - \cos(\phi + \psi)) $$ where $\psi$ is the angle between the radii through the center of mass of the ball and through the center of mass of the trough, $m$ is the mass of the ball, $r$ is its radius, $Ib$ is its moment of inertia. The complicated bit seems to be getting the kinetic energy right since the velocity of the ball is the combination of the ball's center of mass due to the rolling motion of the ball and the velocity of the point of contact between the ball and the trough wall. Well, and the kinetic energy due to the ball's rotation.

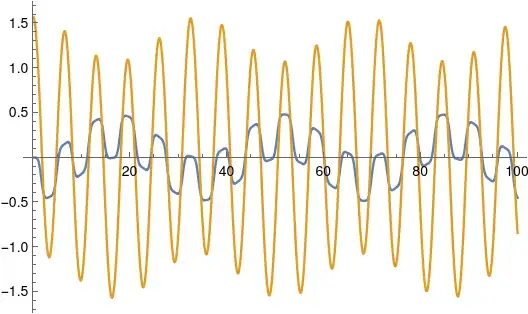
Forming the Lagrangian $$ L=T_t+T_b-(U_t+U_b) $$ and solving the system of resulting equations $$ \frac{\partial L}{\partial q}-\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}=0 $$ where $q=(\phi,\psi)$, I get a system of second order ODEs. Solving the equations numerically (using Mathematica), I get solution plots for $q$ that look like:

Enter image description here

This, however, does not match observed experiments in which the amplitudes of the oscillations of the ball and the trough grow and decay out of phase. It seems unlikely (though perhaps possible) that these changes in amplitude are caused by friction, which is not modeled in the above equations. If the amplitude modulation is not due to friction there must be a bug in my energy equations that I'm failing to spot.

Energy plot looks constant within the numerical precision: Total system energy

I believe I have found the error by comparing to this write-up on dynamics of a cylinder rolling within a cylinder (an obviously connected problem). In summary, the issue is that the ball's angular velocity is computed in a non-intertial coordinate system. I will post a detailed answer shortly.

Daniel Genin
  • 201
  • Is the total energy remain constant ? – Eli Jan 30 '23 at 08:12
  • @Eli Yes, the total energy should be conserved. – Daniel Genin Jan 30 '23 at 14:59
  • Can you plot it ? – Eli Jan 30 '23 at 19:20
  • 1
    FYI, "troth" is an archaic word meaning "loyalty". I think you mean "trough". – Michael Seifert Feb 01 '23 at 12:57
  • 1
    @MichaelSeifert That's a bit embarrassing. Thank you for catching this. – Daniel Genin Feb 01 '23 at 14:07
  • There seems to be a high degree of *dampening* (friction, etc.) in the real system. That does not seem to be captured in this model. A steel ball, more accurately machined parts, lower tolerances (e.g., the distance between the rails), less extreme geometry, and a harder surface (it seems to be wood) would probably look quite different (in the same amount of time). – Peter Mortensen Feb 02 '23 at 16:19
  • @PeterMortensen This is a possibility i'm considering. I'm currently working on a setup that will reduce friction. One of the problems i have already encountered is that if friction between ramp and table is too low then the ramp slides in addition to rolling. – Daniel Genin Feb 06 '23 at 00:35
  • The problem is reminiscent of a double pendulum. There are presumably two modes of vibration for small displacements, one with the ball and cylinder in phase and a second one with them out of phase - and with two different frequencies. Possibly, the boundary conditions used in your model (ball stationary and at max. displacement, cylinder stationary and at min. displacement) have forced the solution to resonate at only one of these frequencies, whereas the physical solution, with its much more chaotic looking appearance, always ends up as a mixed solution. – Penguino Feb 06 '23 at 00:58
  • @Penguino I experimented with multiple different initial conditions and system parameter combinations but the system always remains phase-locked. – Daniel Genin Feb 08 '23 at 20:22

1 Answers1

3

$\def \b {\mathbf}$

enter image description here starting with the position vector $~\b R_b~$ to the cylinder CM $$\b R_b=\b R_p+\b R_c+\b R_r= \left[ \begin {array}{c} R\varphi -\sin \left( \psi \right) R+\sin \left( \psi \right) r\\ R-\cos \left( \psi \right) R+\cos \left( \psi \right) r\end {array} \right] $$ where (equations) $$\b R_p= \left[ \begin {array}{c} R\,\varphi-c\sin \left( \varphi \right) \\ R-c\cos \left( \varphi \right) \end {array} \right]\\ \b R_c=\left[ \begin {array}{c} c\sin \left( \varphi \right) \\ c\cos \left( \varphi \right) \end {array} \right] \\ \b R_r= \left[ \begin {array}{c} - \left( R-r \right) \sin \left( \psi \right) \\ - \left( R-r \right) \cos \left( \psi \right) \end {array} \right] $$

thus the kinetic energy $~T_b~$ and the potential energy $~U_b~$ are:

$$T_b=\frac 12 \,m\b v_b\cdot\b v_b+\frac 12 I_b\dot\phi^2\\ U_b=m\,g\,\left(R_b\right)_y$$

where

$$\b v_b=\frac{\partial \b R_b}{\partial \varphi}\,\dot\varphi+ \frac{\partial \b R_b}{\partial \psi}\,\dot\psi$$

additional from the rolling condition you obtain

$$\b v_b\cdot \hat{\b{t}}_b -r\,\dot\phi=0\quad,\Rightarrow\dot\phi=\frac Rr\,\sin(\psi)\,\dot\varphi$$ where $~\b t_b=[\sin\psi)~,\cos(\psi)]^T~$ is the tangent vector at the contact point between the ball and the cylinder.

with $$T_p=\frac 12\,{p\varphi }^{2} \left( M{R}^{2}-2\,MRc\cos \left( \varphi \right) +M{c}^{2}+{\it Ic} \right) +\tau_{\rm CM}\,\varphi \\ U_p=Mg \left( R-c\cos \left( \varphi \right) \right)$$

you obtain the Lagrange $~\mathcal L=~T_b+T_p-(U_p+U_b)~$ and the equations of motion $~\ddot\varphi=\ldots~,\ddot\psi=\ldots~$

The numerical simulation

with applied torque an the center of mass $~\tau_{\rm CM}$ you obtain

Center of mass Position (Vector $~\b R_p~$)

enter image description here

Center of mass Position (Vector $~\b R_b~$)

enter image description here

enter image description here

Eli
  • 11,878
  • The rolling constraint for the ball assumes that $v_b$ is tangent to the surface of the trough, no? But that doesn't seem to be necessarily the case. – Daniel Genin Mar 06 '23 at 15:07
  • @DanielGenin rolling condition means, that the relative velocity at the contact point P is zero . Perhaps is this equation better ? $~\vec v_b\cdot \hat t-\dot\varphi r=0~$ where t is the tangent vector at the contact point – Eli Mar 06 '23 at 18:22
  • Yes, that makes sense, but is $\vec{v}_b\cdot\vec{t}=|\boldsymbol{v}_b|$? – Daniel Genin Mar 06 '23 at 21:24
  • 1
    Use this constraint equation $~ v_{x}\cos\left( \psi \right) +v_{y}\sin \left( \psi\right) -\dot\phi r=0~$ . I will correct my answer soon – Eli Mar 06 '23 at 22:34