9

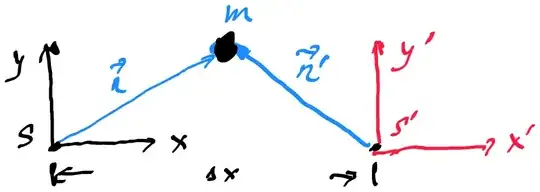
If energy depends on frame of reference of observer, then how it can remain conserved?
Same question also for linear and angular momentum.

I think energy is conserved when seen from a specific frame of reference, but I have doubts about it.

If that's the case, then I think that the energy difference between two systems, when observed from the same frame of reference, remains same for all reference frames, and this energy difference is a more fundamental quantity and it should remain conserved instead.

Kindly explain this to me.

JoSSte
  • 103
Quant2
  • 91
  • 2
    Related: https://physics.stackexchange.com/q/51220/226902, https://physics.stackexchange.com/q/692210/226902, and https://physics.stackexchange.com/q/681167/226902 – Quillo Apr 19 '23 at 12:13
  • 6
    A quantity being "conserved" is not the same as a quantity being "invariant"! "Invariant" means being the same in all frames. "Conserved" means retaining the same value, in any given frame, under physical processes. Kinetic energy is not invariant – it has different values in different frames. But with elastic collisions it will be conserved in each frame. – printf Apr 20 '23 at 07:29

5 Answers5

26

You need to distinguish between the two concepts of 'invariance' and 'conservation'. They are not the same. Invariance is when a quantity is invariant under some kind of transformation. This transformation does not depend on when you make measurements: whether it is before or after a reaction/experiment. Conservation is when a quantity is conserved before and after a reaction (given that you have already chosen a reference frame once and for all, before performing the experiment).

You can have $4$ types of quantities in physics:

  1. Those that are conserved and invariant
  2. Those that are conserved but not invariant
  3. Those that are not conserved but are invariant
  4. Those that are neither conserved nor invariant

Energy is a quantity that is conserved before and after a reaction, but it is not invariant (because you can always go to a new, boosted reference frame).

Avantgarde
  • 3,832
  • 1
    I can't understand the the third type physical quantity you mentioned as if a thing is invariant then it would not vary in any time during the experiment, so it can't vary even during the beginning and end of the experiment and so an invariant thing must be conserved. – Quant2 Apr 19 '23 at 09:37
  • 4
    Mass is invariant (it is Lorentz-invariant). This means that it is the same in different reference frames related to each other by Lorentz transformations. But it is not conserved, because it can be created or destroyed. – Avantgarde Apr 19 '23 at 10:11
  • 4
    @Quant2 That's because you're using the common meaning of "invariant". In physics, "invariant" doesn't mean "something that can't change" (for a given reference, that will rather be "conserved"), it means "something that is the same, at a given moment, for all reference". (I use the word "reference" broadly here, the real definition is with a transformation, which again has, in physics, a different meaning than the common one.) – Blackhole Apr 19 '23 at 21:15
  • 2
    I understood the question as being something like "if I, the observer, boost myself to another reference frame during the experiment, then the energy of the system I'm observing will seem to change; how can we account for that?" Maybe I'm wrong about that being the question, but I feel the answer would be improved if it would address that. – N. Virgo Apr 20 '23 at 03:42
  • @Avantgarde how can I create or destroy mass? – user253751 Apr 20 '23 at 09:59
  • @user253751 With nuclear reactions. – Volker Siegel Apr 20 '23 at 11:54
  • @VolkerSiegel really? which nuclear reaction creates mass from nothing or destroys it? – user253751 Apr 20 '23 at 11:55
  • 1
    @user253751 The energy in nuclear fission and nuclear fusion, in weapons and in power plants, comes from mass that is lost. Very little mass. You split a Uranium nucleus, and the resulting particles have a slightly lower mass together than the original nucleus. The Hiroshima bomb converted a little more than half a gram of mass to energy. – Volker Siegel Apr 20 '23 at 12:03
  • Creating mass happens more often in star explosions than on earth, I think. – Volker Siegel Apr 20 '23 at 12:04
  • @VolkerSiegel energy is mass. How can the energy come from energy that is destroyed? – user253751 Apr 20 '23 at 12:07
  • @user253751 I thought the question implies assuming energy is not mass. – Volker Siegel Apr 20 '23 at 12:13
  • Proper time is a better example of a type 3 quantity. Proper time is the prototypical invariant quantity, all frames agree on it. But it is continuously increasing, so it is clearly not conserved. – Dale Apr 20 '23 at 12:15
  • @user253751 It is less confusing to think of rest mass as a form of energy that is rather difficult to convert to and from. The energy of a system in its rest frame of reference is a Lorentz invariant on top of being conserved, and that value is used to define the rest mass of the system. As for converting the mass energy into other forms, particle antiparticle annihilation converts it 100%, dropping something into a black hole does next best at a few percent, and the general other kinds of nuclear reactions convert small amounts but detectable and detected. – naturallyInconsistent Apr 28 '23 at 02:25
9

No, the energy difference is not more fundamental, and will transform when you change from one frame of reference to another.

All those covariant conserved quantities, energy, momentum, angular momentum, etc, are conserved for every single frame of reference. That is, if you do not change your frame of reference, you will get the same number if you calculated early or late in an experiment. But you cannot compare from one frame of reference to another, unless you transform them correctly.

Volker Siegel
  • 3,883
naturallyInconsistent
  • 8,634
1

I think a good way to think about it is independent of relativity. For an elastic ball bouncing on up and down, energy is conserved. But the value of the energy itself is different based on how you define the potential energy (for example one can choose the potential energy based on height from ground, or from the top of a pole, or say the GMm/R formula using distance from center of earth). Based on your chosen coordinate system, the energy can be different but in a given coordinate system it is conserved (unchanging across time). Something being relative is somewhat similar in that observers who use different frames of reference (imagine them as coordinates) will not agree on the value of it; however the quantity itself is conserved if you stay in the same reference frame/coordinate system.

ssj009
  • 33
0

Lets look at this example

enter image description here

The particle energy in S frame is

$$E_s=\frac 12 m \mathbf v_s\cdot \mathbf v_s+m\,g\,y=\text{const.}$$

where $~\mathbf v_s=\frac{d}{dt}\mathbf R~$

The particle energy in S' frame is

$$E_s'=\frac 12 m \mathbf v_s'\cdot \mathbf v_s'+m\,g\,y'$$

where

$$\mathbf v_s'=\frac{d}{dt}\begin{bmatrix} R'_x+\Delta x \\ R'_y\\ \end{bmatrix}$$ thus, the particle energy $~E_s'~$ is conserved (constant) only if $~\Delta x=v_x\,t~$ or $~\Delta x=~$ constant, where $~v_x~$ constant, in this case is also the energy different ($~\Delta E=E_s'-E_s~$ relative energy) conserved.

is the energy invariant ? invariant mean that $~E_s=E_s'~$ this is not the case.

but if $~\Delta x~=$ const. and $~\mathbf R=\mathbf R'~$ then the energy $~E_s=E_s'~$ (invariant)

Fazit

the "frames energies" can be

  • conserved and invariant
  • only conserved
  • only invariant
  • neither conserved neither invariant
Eli
  • 11,878
0

EN: The question is not well formulated at all and this is because you are not constructing the question from the relativistic point of view; in order that your doubts do not arise with respect to a model or theory, you should put the question correctly in terms of the language of a given theory, in this case special relativity. In fact, the question would be: what are the invariants for all inertial observers (i.e. what are the mechanical invariants of the special theory of relativity)? The answer is : for real particles (not virtual) these invariants are the squares of the linear quadrimomentum, of the angular quadrimomentum among others (the ones that concern your question); in the definition of these quantities are included the energies and the momentum associated to the linear and angular translations respectively; in conclusion neither the linear nor angular energies nor the respective momentum are conserved but other things: the squares of the linear and angular quadrimomentum. I recommend you to read Landau Lifschitz Mechanics / the invariants of a system are associated to its symmetries only and this only in the context of all inertial reference systems.

ES: La pregunta no esta bien formulada del todo y esto se debe a que No estas connstruyendo la pregunta desde el punto de vista relativista;para que tus dudas no se presenten respecto a un modelo o teoria , debes plantear la pregunta correctamente en terminos del lenguaje propio de una teoria dada, en este caso la relatividad especial. Efectivamente la pregunta seria mas bien ; cuales son las invariantes para todos los observadores inerciales ( es decir cuales son las invariantes por ejemplo mecanicas de la teoria especial de la relatividad?). La respuesta es :para particulas reales (no virtuales) dichas invariantes son los cuadrados del cuadrimomentum lineal,del cuadrimomentum angular entre otras (las que conciernen a tu pregunta); en la definicion de esta cantidades estan incluidas las energias y los momentum asociados a las traslacion lineal y angular respectivamente; en conclusion no se conservan las energias lineal ni angular ni los momentum respectivos sino otras cosas: los cuadrados de los cuadrimomentum lineal y angular. Te recomiendo leer Mecanica Landau Lifschitz / las invariantes de un sistema estan asociadas a sus simetrias unicamente y esto solo en el contexto de todos los sistemas de referencia inerciales.

Quillo
  • 4,972
oscar cepeda giraldo
  • 43