About the alleged duplicates: " Quantum entanglement vs classical analogy" "Show quantum entanglement to a classical thinker" refer to black and white balls that would have a correlation at time zero, and this "anticorrelation of color" would be maintained later on. Clearly, if you read what I'm talking about, I am giving the EXACT OPPOSITE analogy of a classical system that does NOT return anticorrelation all the time. On the contrary, it returns different correlation values depending on the axis used for each detector. So while I understand you don't want duplicates, this seems like an exageration to consider my question to be similar to those ones.
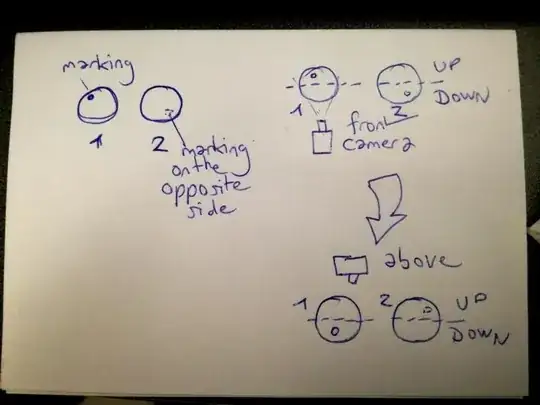
On the above illustration, two spheres have a marking on the opposite side of each other. In the top right corner, we take a picture of sphere 1 and 2 from the front. We observe that in sphere 1 photo, the marking is in the upper half of the picture. We decide to label it as "spin up state". On sphere 2 photo, the marking is on the lower half of the picture. We label it "spin down state". So we have an anticorrelated spin state of sort.
Now, instead of taking pictures in the same axis, we take a picture of sphere 2 from above. And we observe the resulting picture has a 50% chance of returning a spin up or down state, i.e. we lost correlation.
As far as I understand, this is what happens when two particles are entangled and two detectors are set to measure their spin state. If both detectors use the same axis, one can observe that particle B has an anticorrelated spin state that the one measured on particle A. But if different axes are used for detection, the correlation is lost.
So my question is this: what makes entanglement different than the classical spheres analogy I gave above?