Pressure experienced due to magnetic force?

Question

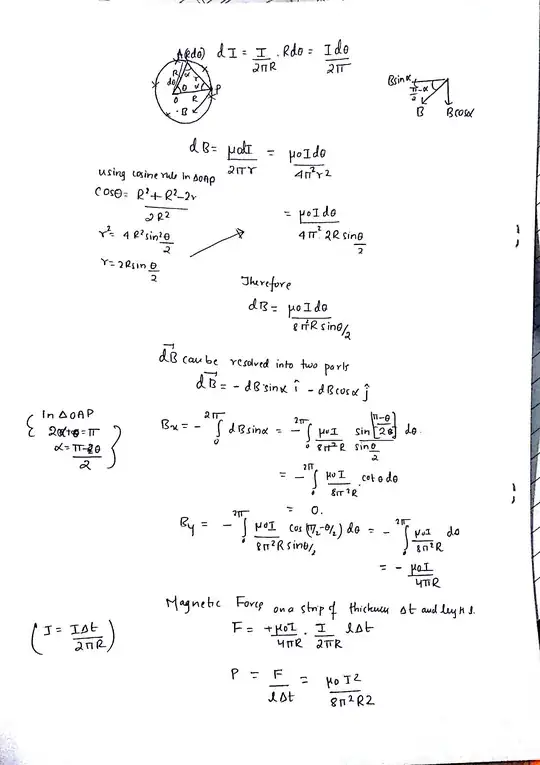
A current $I$ flows in a long thin walled cylinder(parallel to the axis) of radius $R$. What pressure do the walls experience?

This is the 263^rd problem in Section III from the book 'Problems In General Physics by IE Irodov'.

---

My attempt:

Consider a thin segment of the cylinder parallel to the axis of thickness $Rd\theta$(i.e. subtends $d\theta$ at the center). As the current is uniform, the current in this segment will be $$dI = I\frac{d\theta}{2\pi}$$ The magnetic field $B$ near this segment will be $$B=\frac{\mu_0 I}{2\pi R}$$

Force on a length $l$ of this segment will be $$F=BIl=\frac{\mu_0 I}{2\pi R} I\frac{d\theta}{2\pi} l=\frac{\mu_0I^2ld\theta}{4\pi^2R}$$ Pressure will be $$P=\frac{F}{A}=\frac F{lRd\theta}=\frac{\mu_0I^2}{4\pi^2R^2}$$

---

The answer given in the book is $$\frac{\mu_0I^2}{8\pi^2R^2}$$

There are two problems after this also asking to find the pressure due to magnetic forces, in which my answer differs from the actual answer by a factor of $\frac 12$, just like above. Is there something I am missing in my understanding of pressure?

Answer 1

That is because the magnetic force acting on the infinitesimal surface is not $\mu _0 I^2/2\pi R=B$ but $0.5B$ . The factor of half is present because the field inside the cylinder is zero and outside it, is $B$ and therefore the "average value" is $B/2$ acting on the segment. Actually, a better and correct way of understanding this is by stating the field due to the infinitesimal segment as $B_1$ and the field due to the rest of the cylinder as $B_2$. Then outside the cylinder:-
$$B_1+B_2=B$$
and inside $$B_1 + B_2=0$$.
These equations tell you that $$|B_1|=|B_2|=|B|/2$$ and the $B_2$ component is along the net magnetic field and the $B_1$ component is opposite direction to the net magnetic field(inside the cylinder) and along it (outside the cylinder). The force on the infinitesimal segment is only the $B_2$ component and not $B_1$ component which is it's own field. And thus the factor of $1/2$ in your answer.

Answer 2

I have provided the solution in the image..See basically You are right till the Magnetic field part but You have to mention current in force part in terms of Current Per unit length as u have taken a strip here.. Hope this help

P.S. I know it is late ..4yrs you would've already figured this out P.S. This is for othere who seek this question and I dont think the average concept work here anyway.. Thanks