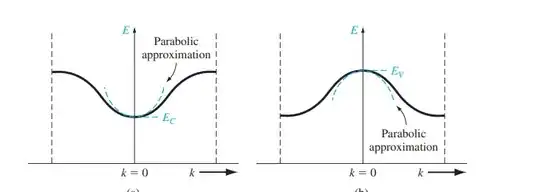
the solution of kroning-penny model inside the semiconductor crystall was something like this
where this solution can be approximated in the conduction band and valence band by a parabola where
\begin{gather*} E=E_{C}+\frac{(\hbar k)^2}{2m} \end{gather*}
where $E_{C}$ is the potential energy of the conduction band and $\frac{(\hbar k)^2}{2m}$ is the Kinetic energy
and also in valence band \begin{gather*} E=E_{V}-\frac{(\hbar k)^2}{2m} \end{gather*}
But the problem is : total energy in the valence band is the summation of kinetic and potential , but the kinetic energy in the valence band is Negative !
This doesn't makes sense because the \begin{gather*} K.E=\frac{p^2}{2m} \end{gather*} which can't be negative
so how this make sense at all?