Why are pressure hulls machined to be nearly spherical?

Question

Why are pressure hulls machined to be nearly spherical? According to Wikipedia, https://en.wikipedia.org/wiki/DSV_Limiting_Factor has a hull that is machined to be nearly spherical "for enhanced buckling stability". Is this really superior to an unmachined hull in terms of pressure resistance?

I can see why it might be useful to trim any excess weight from a diving vehicle, but I don't see how removing material can ever improve pressure resistance. Does anyone have any insights?

Any shape other than a sphere under spherically symmetric compression will have stress concentrations greater than for a sphere. — Jon Custer, Jun 28 '23 at 12:35
@JonCuster But the compression at depth is not "spherically symmetric" if the vehicle is not spherical - rather, it has the same psi everywhere along the shape's surface. The machined hull is always a part within the unmachined hull. I guess the question is can the irregular surface cause any "lensing" of the stress that would make it larger in the unmachined case. — bhuff36, Jun 28 '23 at 13:14
Having the same psi everywhere on the surface is, in fact, spherically symmetric (or close enough). And what the designer worries about is then the impact of that stress on the material itself, which is where your 'lensing' (or stress concentration) comes in to play. Consider using a square instead, and compare what you think will happen at a corner vs in the middle of a face. — Jon Custer, Jun 28 '23 at 13:17
@JonCuster A cubic shell that can be machined down to a spherical shell will necessarily have considerably more bulk. I would think it would have at least equivalent pressure resistance. We can also consider starting from a perfect spherical shell and adding material. What kind of shape should be added to create lensing / stress concentration whereby the augmented shape is less resistant than the original? — bhuff36, Jun 28 '23 at 15:53

score 0 · Answer 1 · answered Dec 17 '23 at 22:44

Pressure acts on surfaces perpendicular to the surface. Therefore in a sphere, the pressure stresses the structure equally around the circumference. Deviations from spherical construction create "stress points", areas where the pressure could separate the structure. Since perfectly spherical construction is rarely desirable, these stress points must be mitigated via additional supporting structure such as additional bulkheads, ribs, stringers, etc. Therefore, spherical construction is leveraged to conserve resources through design (reduced engineering effort) and construction (less material and labor for assembly).

score 0 · Answer 2 · answered Dec 18 '23 at 00:40

I don't think stress concentrators are the main reason for a perfect spherical shell being able to withstand higher external pressure than an imperfect spherical shell in this case. According to the Wikipedia article quoted by the OP, the hull was shaped to a sphere "for enhanced buckling stability". Buckling is a form of failure of vessels under external pressure. One can watch a video of a rail car tank collapsing due to buckling.

The critical pressure of a perfect thin spherical shell for buckling is $$p_{cr}=\frac{2 E h^2}{\sqrt{3(1-\mu^2)}R^2},$$ where $h$ and $R$ are the thickness and the radius of the shell, and $E$ and $\mu$ are the modulus of elasticity and the Poisson’s ratio of the material of the shell.

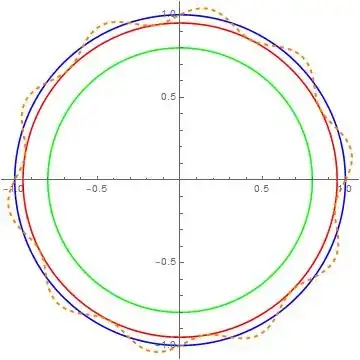
Let us look at the following figure. Let us assume that the initial perfect spherical shell is between the green and the blue lines. Let us also assume that a relevant imperfect spherical shell is between the green and the orange lines. Then machining the imperfect spherical shell to the new perfect spherical shell between the green and the red lines can actually increase the critical buckling pressure as imperfections can easily reduce the critical buckling pressure of a spherical shell by a factor of 0.2, so the shell between the green and the red lines will have lower $p_{cr}$ than the shell between the green and blue lines, as it is thinner, but it can have a higher $p_{cr}$ than the shell between the green and the orange lines.

Why are pressure hulls machined to be nearly spherical?

2 Answers2