I'm curious to learn more about the way that protons, neutrons and electrons interact. Specifically, about how the forces that attract and repel them work.
While I don't have a background in physics or chemistry, I understand that protons have positive charge, electrons have negative charge and neutrons have no charge, and that like charges repel and opposite charge attract. I also understand that all of those particles have mass as well, and that they are all subject to gravitational attractive forces.
The first thing that I don't quite understand is whether these particles actually "collide" with each other when they make up an atom. It's my understanding that protons, neutrons and electrons all have tangible radii. However, I can't really see exactly what happens when they get really close to each other.
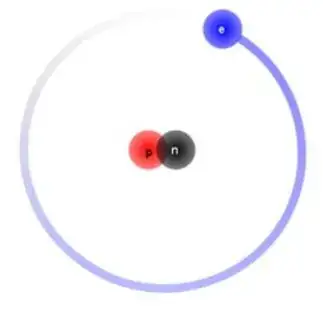
Let's take a Deuterium atom as an example (I'm using the Bohr model diagram of the atom here as an example, but I'm aware that electrons don't actually orbit the nucleus in perfect shells):
My initial rationale when looking at a diagram above is to say that the proton and neutron are able to stick together so tightly because they have higher masses compared to the electron, resulting in higher gravitational forces that the two experience compared to the electron.
However, do the proton and neutron in the example atom above actually go inside each other when they stick together in the nucleus? Do they experience "collision" in the same way that solids do, where they always stay completely outside each other but still close? Is it somewhere in the middle of the two?
Additionally, what happens if an electron passes through the nucleus during it's orbit? Does it "impact" the protons and neutrons, or does it pass through them?
Another thing I'm curious to learn more about is exactly how electrons are able to stray so far away from the nucleus, and not get absorbed into it along with the proton and neutron.
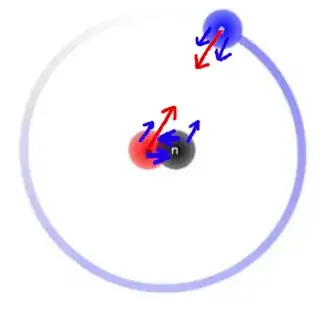
Since the proton and electron have opposite charges, they should attract each other. Combined with the gravitational forces they both experience due to them both having mass, the same Deuterium atom displayed in the previous question should have the following attraction vectors ($\color{blue}{\textrm{blue}}$ arrows show gravitational forces, $\color{red}{\textrm{red}}$ arrows show charge forces & arrow sizes show force magnitudes):
Since the proton and electron both experience charge forces alongside the gravitational forces, is the reason the electron is not as tightly close to the proton as the neutron because the electron has a lower mass compared to the two? Or is there another reason the electron strays so far away from the nucleus despite the attractive forces?
Finally, I wish to learn more about what mathematical formulas are used to represent the two forces mentioned in my previous two questions, and whether there are any other forces that act on these particles as they move around.
I initially assumed that the gravitational force between two particles could be represented by Newton's Law of Universal Gravitation:
$F_{mass} = G*\frac{m_{1}m_{2}}{r^{2}}$
Where $F$ is the force vector in Newtons, $G$ is the gravitational constant of $6.67*10^{-11}$, $m_{1}$ and $m_{2}$ are the masses of the two particles in kilograms, and $r$ is the distance between the centers of the two particles in meters.
I also initially assumed that the charge force could be represented by Coulomb's Law:
$F_{charge} = \frac{1}{4\pi\epsilon_{0}}*\frac{q_{1}q_{2}}{r^{2}}$
Where $F$ is the force vector in Newtons, $\epsilon_{0}$ is the permittivity of free space of $8.854*10^{-12}$, $q_{1}$ and $q_{2}$ are the charges of the two particles in Coulombs, and $r$ is the distance between the centers of the two particles in meters.
However, attempting to use the two equations above to calculate the approximate forces of these particles gets rather strange.
For example, let's suppose we have two protons that are $1*10^{-14}$ meters apart, completely by themselves.
Assuming the charge of a proton is $1.6022*10^{-19}$ C, and the mass of a proton is $1.67*10^{-27}$ kg, the repellant force that each proton experiences is:
$F_{charge} = \frac{1}{4\pi(8.854*10^{-12})}*\frac{(1.6022*10^{-19} C)^{2}}{(1*10^{-14} m)^{2}} = \sim2.307 N$
If we then calculate the acceleration due to the charge force that the protons experience in the opposite directions from each other, we get:
$a_{charge} = \frac{F_{charge}}{m} = \frac{2.307 N}{1.67*10^{-27} kg} = \sim1.381*10^{27} \frac{m}{s^{2}}$
Does this acceleration value due to the charge look correct? If we compare $F_{charge}$ to $F_{mass}$ obtained by Newton's Law of Universal Gravitation:
$F_{mass} = 6.67*10^{-11}*\frac{(1.67*10^{-27} kg)^{2}}{(1*10^{-14} m)^{2}} = \sim1.860*10^{-36} N$
$F_{mass}$ is only $\sim8.06*10^{-35}$ % of $F_{charge}$... If the gravitational force is this much smaller than the charge force, how can the protons inside the nucleus ever stick together?
Are Newton's Law of Universal Gravitation and Coulomb's Law not good representations of the forces that these particles experience? If not, what are the mathematical equations that represent these forces, if any? Are there perhaps other forces that are at play here? If so, what are their mathematical representations?
Thanks for reading my post, any guidance is appreciated.