Well, in simple words, instantaneous velocity is the velocity at a particular instant.
As you may already know, average velocity is defined as total diplacement by total time. Let me explain the idea of instantaneous velocity with the help of an example. Maybe the 2nd graph given in your question.
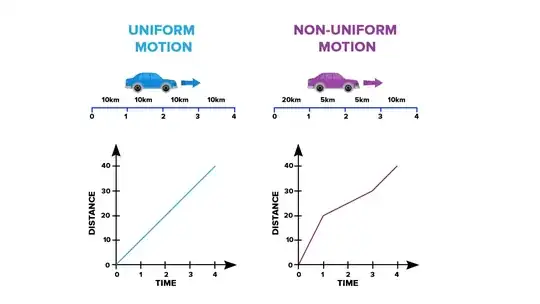
In the second graph of yours the body travels 40 units in 4 secs. Avg velocity in this case is 10 m/s. It's average in the sense that it doesn't exactly tell us what the velocity would be at a particular instant. This problem arises in non-uniform motion as the body moves with variable velocity. So the average velocity doesn't give us an idea of the velocity at a particular instant, say t=1 sec. So answering the latter part of your question: yes, instantaneous velocity can be found out in both- uniform and non-uniform motion. In uniform motion the instantaneous velocity = average velocity at all instants and so it isn't really required. In non-uniform motion (i.e., the second graph), it can be of great help as it can tell us the velocity at a particular instant. It is actually used mostly when the motion is accelerated, i.e., the graph is a curve.
Now, how do you find instantaneous velocity? If you have the knowledge of calculus, it's pretty straightforward. Take the derivative. But in case you don't, here's an interesting approach:
To work up to instantaneous velocity of the body at t = 1 sec, we can use the definition of average velocity.
Since we want the velocity at the instant t = 1 sec let's try working with the formula for avg velocity. Let's check the displacement covered by the body from 0 to 1 sec and divide it by 1 sec. This will give us the avg velocity in this time interval. Intuitively if we keep reducing this time interval we can reach up to the instantaneous velocity of the particular instant. This is based on a concept called 'Limits'.
So keep reducing the time interval. In this case if we check the displacement b/w 0.9999 and 1 sec and divide it by 0.0001 we will see that the value tends to some value. As the time interval is decreased further we come closer to that value. That value is the instantaneous velocity and this exactly is how derivatives work. $\frac{dy}{dx}$ means checking the change in y w.r.t the change x, where change in x approaches 0. In this case as we keep reducing the time interval our answer becomes increasingly accurate.
It's a broad concept and I've tried to explain it in the best possible manner.
Here's a video based on the same:
https://youtu.be/9vKqVkMQHKk?si=YLroVkar5GNVQKmt
Channel: 3blue1brown