It is well known from this famous question that the roots of a random polynomial tend to be close to the unit circle. So I was wondering in a somewhat converse sense: for an irreducible polynomial, is it possible that many roots are collinear (on a line other than the real or the imaginary axis)?
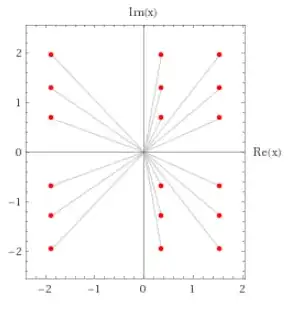
Now, if we take for instance a Chebyshev polynomial $T_k(x^n-1)$, we get trivially $k$ roots on each of the $n$ rays from $O$ through each $n$th root of unity, see e.g. here for $k=5,n=7$ (left picture). But what if we want roots on a line which are not collinear with the origin, i.e. not proportional over $\mathbb R$? (And of course mere linear shifts should be excluded, like replacing in such a polynomial $x$ by $x-1$.)
We can easily get twice four of them on vertical lines, e.g. for the minimal polynomial of $ \dfrac{1+i}{\sqrt[4]{2}}+(\sqrt{2}+1)i $, which is $x^8+12 x^6+16 x^5+42 x^4+32 x^3+68 x^2+112 x+73$ (right picture).
This raises several questions (remember that it is all about irreducible polynomials, so we could talk as well of the Galois conjugates of a given algebraic number):
Assuming that the pattern has no rotational symmetry and taking the word 'line' to exclude both axis,
1. Is it possible to have more than 4 roots on a line?
2. Can a line with 4 or more roots be other than horizontal or vertical? If so, which slopes can occur?
3. Is it even possible to have exactly 3 of the roots on a line?
EDIT: Q1 and Q3 => Yes by Ilya Bogdanov's comments. So Q2 remains, and I've added Q4:
4. Is it possible that the roots make up a $p\times q$ grid where $p$, the number of rows, is not a power of $2$?
Note that there can be patterns with only one line of 4 collinear roots, e-g. the minimal polynomial of $\sqrt{2}+i+ \dfrac{i}{\sqrt[4]{2}} $ , viz. ${ {4 x^8-16 x^6+32 x^5+84 x^4-192 x^3-40 x^2-112 x+353}}$: 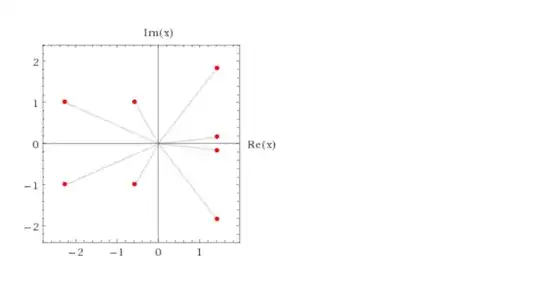
For Q1, it might be possible to find constructions by some sort of "bifurcation" in a sense similar to what happens with the logistic map, but I am not very sure about that. If at all, I'd conjecture that for any [edit: vertical] line, the number of roots it contains always is a power of 2.
EDIT: Q4 has a positive answer. (And so has Q2.) Based on the construction of Jeremy Rouse in the related question, we have e.g. $$x^{18}+6x^{15}+54x^{14}-54x^{13}+24x^{12}+378x^{11}+189x^{10}\\ -1672x^9+5184x^8+162x^7-11649x^6+13824x^5\\ +28944x^4-80904x^3+138240x^2-86400x+44992$$ whose roots come in a nice $3\times 6$ pack as displayed here: