9

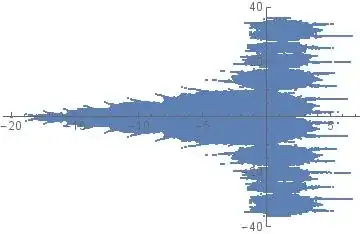
Has the dynamics of the Riemann zeta function been studied? By dynamics I mean the limiting behavior of the sequence of iterates $s, \zeta (s), \zeta (\zeta (s)), \zeta (\zeta (\zeta (s)))\dots $ for various starting values of $s$ in the (extended) complex plane. In particular, for which $s \in \mathbb{C}$ do the iterates $\zeta^{(n)}(s)$ converge to 0?

user137686
  • 91
  • 8
    $\zeta^{(n)}(s)$ can't converge to 0 because $\zeta(0)=-1/2.$ – Alexey Ustinov Mar 30 '19 at 06:04
  • 3
    Because of universality, the study of Zeta iteration is at least as hard as the study of general complex dynamics. – LeechLattice Mar 30 '19 at 07:57
  • 1
    https://www.dhushara.com/DarkHeart/key/key2.htm – Adam Aug 11 '19 at 04:24
  • The convergence to -0.295... is clearly a convergence through Zero. Please read The Towering Zeta Function. By Knuth and others, this means the function convergences to roots that obey a rational exponential function which leads to the half-line. Michael M. Anthony.. – user144937 Aug 26 '19 at 09:44
  • I've been trying to characterise the iteration fractals of the Riemann zeta function (and Hurwitz zeta functions and Dirichlet L functions) for a while. See attached example image(https://i.stack.imgur.com/nUln0.png) and more here: https://primepatterns.tumblr.com/ – user2285332 May 21 '19 at 21:50

2 Answers2

8

One can observe that $s=-0.295905\ldots$ is an attracting fixed point.

One can do computations which give pictures of the Mandelbrot set of this iteration. (points are those which have after 20 iterations an absolute value less than 100.) Pictures of this type were quite popular in the mid 80s, when home computers became widely available.)

iterations of zeta

Here are two items of literature

1) S.C.Woon, Fractals of the Julia and Mandelbrot sets of the Riemann Zeta Function, https://arxiv.org/abs/chao-dyn/9812031

2) Michael M. Anthony, The Towering Zeta Function Advances in Pure Mathematics Vol.06 No.05(2016), Article ID:65860,42 pages 10.4236/apm.2016.65026

http://file.scirp.org/Html/7-5301015_65860.htm

Christian Elsholtz
  • 2,725
4

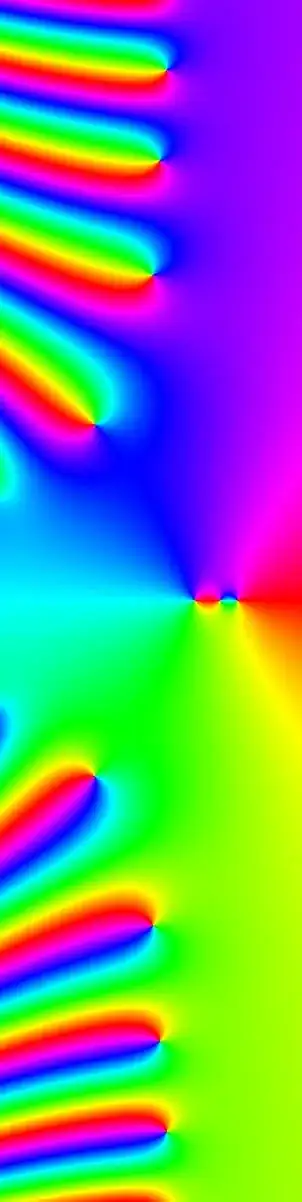
There is also a fixed point near $s=1.83377$. The Mathematica graphic below shows the argument of $\zeta(s)-s$, for $-10\le\sigma\le 5$, $-30\le t\le 30$,interpreted as a color. We see the two real fixed points and the pole at $s=1$, as well as a number of complex conjugate pairs of fixed points.

arg zeta(s)-s

Stopple
  • 10,820