1

Using the following definition of Dirichlet L-function $$ L(1,\chi)=\begin{cases} \dfrac{2\pi h}{w\sqrt{m}} & \textit{if}\ \chi(-1)=-1 \\\\ \dfrac{2 h \log{|\epsilon|}}{w\sqrt{m}} & \textit{if}\ \chi(-1)=1 \\ \end{cases} $$ and Theorem 4 of Yitang Zhang latest results on Landau–Siegel zero, I have derived the 2 following discrete maps (I called them Yitang dynamics): $$ x_{n+1}=\frac{\beta}{\sqrt{x_n}}+c\log(x_n)^{-\alpha},\quad \chi(-1)=-1 \tag{1}\label{1} $$ with $x_n=m,n=0,1\dotsc$ and $\beta=\frac{2\pi h}{w}$ , $c$ is the constant of Yitang defined in his Theorem 4.

For the second case $\chi(-1)=1$, Yitang dynamics can be written as : $$ x_{n+1}=\frac{\beta \log(|\epsilon|)}{\pi\sqrt{x_n}}+c\log(x_n)^{-\alpha},\quad \chi(-1)=1. \tag{2} $$ Edit: The discussion and analysis of this dynamics is montioned here on my Wordpress blog and for more detail one can check my arXiv paper entitled New chaotic dynamics for Yitang Zhang latest results on Landau–Siegel zero.

Yitang discrete dynamics seems to have a fixed points converge to 0 as shown in the below figure:

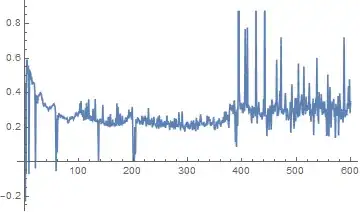
Edit: Some Lyapunov exponents of Yitang dynamics (numerical data) for $\alpha$ in the range $(0,600)$ have been computed using Mathematica code available here as a notebook, see the interpreted data in the following plot:

enter image description here

Now my partial questions here according to the above analysis are:

Question: Assume the dynamics \eqref{1} is reformulated correctly. Is there any relationship between analytical solutions of dynamics \eqref{1} and Landau–Siegel zero? Is it possible to compute the entropy of that dynamics? Does the chaotic behavior of this dynamics give any validity about Yitang latest results on Landau–Siegel zero?

Note1: for more explanation for Entropy I want to compute is the entropy of Kolmogorov Sinaiit is known that Kolmogorov Sinai entropy $H_{KS}$ is bounded by the sum of positive Lyapunov exponents due to the Margulis-Ruelle inequality, I'm not able to get such closed form expression for the values of Lypunove exponents I got here for getting the upper bound of Kolmogorov Sinai entropy , and my purpose for that is to know more about injectivity and bijectivity for Yitang dynamics.

Note2: the motivation behind this question is to predict such relationship between Landau–Siegel zeros and the analytical solution of the reformulated discrete dynamics.

Reference:

(1): Dynamics of Riemann zeta function

(2): Contribution of Yitang Zhang latest results if correct to correlation conjecture of H. L. Montgomery?

David Roberts
  • 33,851
zeraoulia rafik
  • 2,236
  • Should it be obvious that there's any connection at all? More specifically, why should that choice of $c$ be meaningful to the dynamics whatsoever? (plenty of dynamical systems exhibit regions of stability, so a more fundamental reason than that would be needed) – Brevan Ellefsen Apr 06 '23 at 03:37
  • 2
    @BrevanEllefsen I didn't claimed that it should there is a clear connection (I aslo asked about that), since roughly the dynamics were derived from the definition of L function and Theorem of Yitang latest on Landau siegle zero(please check the above linked theorem 4) and for c it is the effective absolute constant of yitang in His theorem that just positive you may need take it as you want , you will get the same behavior and similar analyze. – zeraoulia rafik Apr 06 '23 at 04:35
  • 2
    For example, "entropy" can mean many things to different people. So it is better to write down the mathematical definition you have in mind. – Thomas Kojar Apr 08 '23 at 20:22
  • 1
    MO is not really a place for presenting research. But if you get stuck on some technical question, please free to post it. – Thomas Kojar Apr 08 '23 at 20:26
  • @ThomasKojar ,Thank you , I already wrote a priprint i submitted to arxiv 2 days ago , For Entropy i think it's clear that i mean entropy of discrete map which is less than or equal's sum of Lypunov exponents ,but am going to add some detail in the above question – zeraoulia rafik Apr 08 '23 at 20:30
  • Still you need to add more mathematical-symbols and definitions (eg. of entropy) in your questions. These current questions seem open-ended. – Thomas Kojar Apr 08 '23 at 20:57
  • @ThomasKojar, Thanks for your attention .am going to add this – zeraoulia rafik Apr 08 '23 at 20:58
  • 1
    For example, if you are trying to prove some math-theorem, specify any steps that you are stuck on. eg. "I tried to compute the entropy using Lyapunov exponents, but I got stuck at getting an upper bound here." – Thomas Kojar Apr 08 '23 at 20:59
  • @ThomasKojar, I wish what i have added about entropy for more clarification is enough – zeraoulia rafik Apr 08 '23 at 21:24
  • We will see what experts think. It wouldn't hurt to add some of your own mathematical-attempts to get that upper bound/closed-expression you mention and explaining what mathematical/technical issues arise. The more math symbols you add, the more concrete your questions will be. – Thomas Kojar Apr 08 '23 at 22:01
  • @ThomasKojar ,am still awaiting their comments .unfortunately i have got no comment even now ,I sent a copy of my arxiv paper to Yitang Zhang and i wish to receive his comments to improve my paper. – zeraoulia rafik Apr 11 '23 at 23:11
  • 2
    MO is more about answering specific technical questions and less about presenting research or conjectures ("does A relate to B?"). If you try to prove some theorem and you get stuck, please feel free to post here. – Thomas Kojar Apr 12 '23 at 00:08
  • @ThomasKojar, That is just few results not all research , I think that is allowed to discuss results by presenting partial questions , look for example Yitang Zhang results are presented in the context of partial questions, I already added them as reference – zeraoulia rafik Apr 12 '23 at 01:27

0 Answers0