$f(f(x))=\exp(x)-1$ and other functions "just in the middle" between linear and exponential

Question

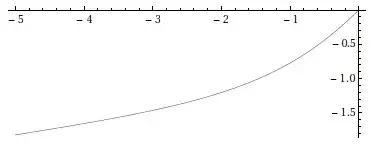
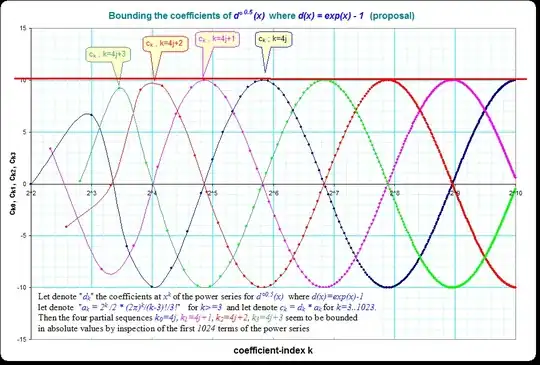
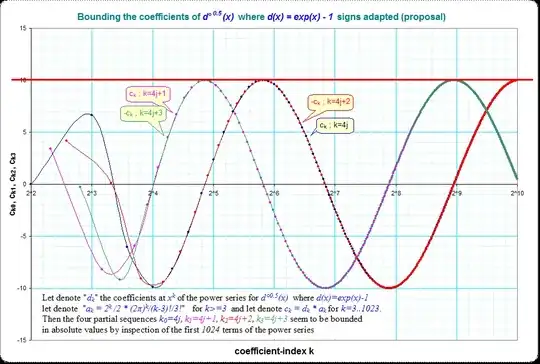
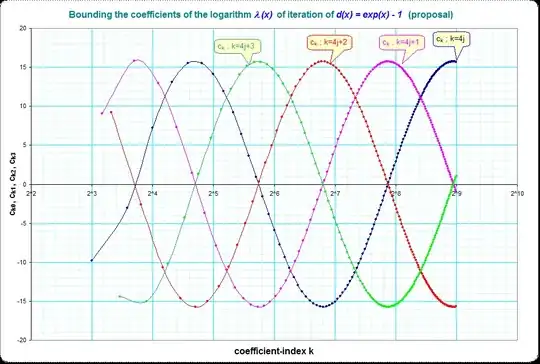
The question is about the function $f(x)$ so that $f(f(x))=\exp (x)-1$.

The question is open ended and it was discussed quite recently in the comment thread in Aaronson's blog here http://scottaaronson.com/blog/?p=263

The growth rate of the function $f$ (as $x$ goes to infinity) is larger than linear (linear means $O(x)$), polynomial (meaning $\exp (O(\log x)))$, quasi-polynomial (meaning $\exp(\exp O(\log \log x))) $ quasi-quasi-polynomial etc. On the other hand the function $f$ is subexponential (even in the CS sense $f(x)=\exp (o(x))$ ), subsubexponential ($f(x)=\exp \exp (o(\log x))$) subsubsub exponential and so on.

What can be said about $f(x)$ and about other functions with such an intermediate growth behavior? Can such an intermediate growth behavior be represented by analytic functions? Is this function $f(x)$ or other functions with such an intermediate growth relevant to any interesting mathematics? (It appears that quite a few interesting mathematicians and other scientists thought about this function/growth-rate.)

Related MO questions:

• solving $f(f(x))=g(x)$
• How to solve $f(f(x)) = \cos(x)$?
• Does the exponential function has a square root
• Closed form functions with half-exponential growth
• $f\circ f=g$ revisited
• The non-convergence of f(f(x))=exp(x)-1 and labeled rooted trees
• The functional equation $f(f(x))=x+f(x)^2$
• Rational functions with a common iterate
• Smoothness in Ecalle's method for fractional iterates.

Answer 1

Let me see if I can summarize the conversation so far. If we want $f(f(z)) = e^z+z-1$, then there will be a solution, analytic in a neighborhood of the real axis. See either fedja's Banach space argument, or my sketchier iteration argument. The previous report of numerical counter-examples were in error; they came from computing $(k! f_k)^{1/k}$ instead of $f_k^{1/k}$. We do not know whether this function is entire. If it is, then there must be some place on the circle of radius $R$ where it is larger than $e^R$. (See fedja's comment here.)

If we want $f(f(z)) = e^z-1$, there is no solution, even in an $\epsilon$-ball around $0$. According to mathscinet, this is proved in a paper of Irvine Noel Baker, Zusammensetzungen ganzer Funktionen, Math. Z. 69 (1958), 121--163. However, there are two half-iterates (or associated Fatou coordinates $\alpha(e^z - 1) = \alpha(z) + 1$) that are holomorphic with very large domains. One is holomorphic on the complex numbers without the ray $\left[ 0,\infty \right)$ along the positive real axis, the other is holomorphic on the complex numbers without the ray $\left(- \infty,0\right]$ along the negative real axis. And both have the formal power series of the half-iterate $f(z)$ as asymptotic series at 0.

If we want $f(f(z))=e^z$, there are analytic solutions in a neighborhood of the real line, but they are known not to be entire.

I'll make this answer community wiki. What else have I left out of my summary?

Here is a related MO question. The answers to the new question contain further interesting information. Let me mention here a link with many references on "iterative roots and fractional iterations" one particular link on the iterative square root of exp (x) is here.

The following two links mentioned in the old blog discussion may be helpful

• http://www.math.niu.edu/~rusin/known-math/97/sqrt.exp (outdated link)

• http://www.math.niu.edu/~rusin/known-math/99/sqrt_exp (outdated link)

• http://web.archive.org/web/20140521065943/http://www.math.niu.edu/~rusin/known-math/97/sqrt.exp

• http://web.archive.org/web/20140521065943/http://www.math.niu.edu/~rusin/known-math/99/sqrt_exp

Answer 2

Allow me to leave alone the particular equation you mention and the issue of series, and focus instead on the general idea of finding functions "in the middle" between two families of functions. There is some extremely interesting mathematics in that idea.

The essence of this part of your question is that you have two families of functions, in your case the linear functions and the exponential functions, and the first family lies below the second in the sense that every function in the lower family is eventually dominated by every function in the upper family. Because of this, it is very natural to want to understand the functions that lie between the two classes. In what circumstances and for which types of families $L$ and $U$ can we always find a function $f$ filling the gap? That is, we seek a function $f$ that eventually dominates the functions in the lower family $L$ and is eventually dominated by the functions in the upper family $U$. It is natural to consider the cases where the families are maximal in some sense, and as a special case, one might consider what happens when they are linearly ordered by eventual domination.

Much of the content of this question is present already in the case of functions $f:\mathbb{N}\to \mathbb{N}$, and indeed, it turns out that much of the fundamental phenomenon occurs already for functions $g:\mathbb{N}\to 2$, which amounts to considering the quotient $P(\omega)/Fin$, as in this MO answer.

This way of thinking is intimately connected with the phenomenon of Hausdorff gaps.

• First, if both families are countable (or are determined by a countable sub-family, which is true in your case), then it is an enjoyable exercise to show that one may always fill the gap (first proved by Hausdorff). That is, given two countable families of functions, members of the first always eventually dominated by members of the second, then there is a function filling the gap.

• Second, Hausdorff constructed examples of families of functions that do not admit any function in the middle; these gaps cannot be filled. That is, he produced a lower family $L$ and and upper family $U$, such that every function in the lower family was eventually dominated by every function in the upper family, but there is no function just in the middle, filling the gap. His examples were unfilled gaps having uncountable order type $(\omega_1,\omega_1)$, in the sense that the both the lower and upper families are determined by an almost-increasing $\omega_1$-sequence of functions.

• The unfillable nature of these gaps, however, admits extensive set-theoretic independence, in the sense that an unfilled gap can sometimes be filled by a function that is added by forcing, that is, by moving to a larger set-theoretic universe. At the same time, there are methods of sealing a gap, that prevent it from ever being filled in a cardinal-preserving forcing extension.

• Kunen proved that it is consistent with Martin's axiom plus $\neg CH$ that there are unfilled gaps of type $(\omega_1,c)$ and $(c,c)$, where $c$ is the continuum, and also consistent that all such gaps are filled.

Answer 3

There is a unique formal power series solution with $f(0) = 0$ and $f'(0) = 1$. I had supposed that the coefficients would all be positive, which would imply that they are smaller than for $\exp(x)$ itself and thus that $f(x)$ is entire. No such luck. Maple gives me this:

$$f(x) = x + \frac{x^2}4 + \frac{x^3}{48} + \frac{x^5}{3840} - \frac{7x^6}{92160} + \frac{x^7}{645120} + \frac{53x^8}{3440640} + \cdots.$$

This doesn't say much about the possible radius of convergence of this series. On the other hand, expecting it to be entire may have been naive from the beginning, because it seems unlikely that $f(f(x))$ would be periodic in the imaginary direction.

---

Since Michael Lugo has found evidence that the Taylor series has zero radius of convergence, it's not a very good way to describe or even define $f(x)$. Is it clear that there is a unique $f(x)$ which is convex (at least for $x \ge 0$), and that that $f$ is smooth at 0 and real analytic away from $0$? There is a book on fractional iteration of functions that presumably addresses these issues.

Answer 4

If all you want is a compositional square root of something like $e^z-1$ analytic in some disk around the origin, I would go for $e^z-1-\frac 34 z=\frac z4+h(z)$. Then, putting $f(z)=\frac z2+g(z)$, we see that we need to solve $$ g(z)=Tg(z)=-2g(\tfrac z2+g(z))+2h(z). $$ Now consider the Banach space of all analytic in the disk $D$ of radius $r>0$ functions $g$ satisfying $\|g\|= \sup_{D}|g(z)|\cdot|z|^{-3/2}<+\infty$. If $r$ is small enough, then $T$ maps the unit ball in this space to itself and is a contraction there.

Answer 5

This doesn't seem to be immediately germane to complexity theory, but the specific case of exp(x)-1 is somewhat interesting from the standpoint of formal groups. exp(x)-1 gives a distinguished isomorphism between the formal additive group law and the formal multiplicative group law (and such an isomorphism only exists in characteristic zero). There are two square roots of this isomorphism, yielding intermediate formal group laws. For each prime p, both isomorphisms converge on a p-adic disc of small positive radius. Similar behavior holds for n-th roots.

Answer 6

Consider $g(x)=e^x-1$. Then $g^n(x)= x+\frac{1}{2!}n x^2+\frac{1}{3!} \left(\frac{3 n^2}{2}-\frac{n}{2}\right) x^3+\frac{1}{4!} \left(3 n^3-\frac{5 n^2}{2}+\frac{n}{2}\right) x^4 $ $+\frac{1}{5!} \left(\frac{15 n^4}{2}-\frac{65 n^3}{6}+5 n^2-\frac{2 n}{3}\right) x^5 $

$ +\frac{1}{6!} \left(\frac{45 n^5}{2}-\frac{385 n^4}{8}+\frac{445 n^3}{12}-\frac{91 n^2}{8}+\frac{11 n}{12}\right) x^6 $

$ +\frac{1}{7!}\left(\frac{315 n^6}{4}-\frac{1827 n^5}{8}+\frac{6125 n^4}{24}-\frac{1043 n^3}{8}+\frac{637 n^2}{24}-\frac{3 n}{4}\right) x^7 + \cdots$

Note that $g^0(x)=x, g^1(x)=e^x-1$ and that

$g^\frac{1}{2}(x)=x+\frac{x ^2}{4}+ \frac{x^3}{48} +\frac{x^5}{3840}-\frac{7 x^6}{92160} +\frac{x^7}{645120}$ which is consistent with what Greg Kuperburg obtained. A symbolic mathematical program will also confirm that $g^m(g^n(x))=g^{m+n}(x) +O(x^8)$

See The Euler-Arnold equation for more information.

Answer 7

You can find the half-iterate of a function from known integer iterates by using Newton series, for example:

$$f^{[1/2]}(x)=\sum_{m=0}^{\infty} \binom {1/2}m \sum_{k=0}^m\binom mk(-1)^{m-k}f^{[k]}(x)$$

This does not converge for $f(x)=a^x$ where $a>e^{1/e}$ but since your function is somewhat different you can try this method.

Update. Here is a plot for $x<0$:

    (source)

For positive $x$ it seems the formula mostly does not converge.

Answer 8

I'd like to answer to Anixx's post of 3 nov 2010, but do not see how I could append it properly to his comment, sorry. For the comparision of the Newton-formula for the half-iterate and the formula in the version of D.Geisler (which can be obtained using matrix-logarithm on the Bell-matrix for exp(x)-1) and for more general b^x-1 by diagonalization I wrote an article on my homepage, see

http://go.helms-net.de/math/tetdocs/BinomialDiagonalization.htm

It shows, that the Newton-method needs more terms than that of the diagonalization-method and narrows an interval. It appears heuristically, that the Newton-formula converges to that of the diagonalization method and that the diagonalization-method is "immediately" in the center of that narrowing interval (giving a precise approximation very early)

---

In the earlier comments it was mentioned, that I.Baker proved the zero-radius of convergence of the formal powerseries for the fractional iterates of exp(x)-1 . In 2008 I've done a little study of that property of the involved formal powerseries and analyzed the growthrate of coefficients. An explanation is in

http://go.helms-net.de/math/tetdocs/CoefficientsForUTetration.htm

(I just updated the earlier version)

More numerical examples are in

http://go.helms-net.de/math/tetdocs/htmltable_utetrationFractionalIteration.htm

I'd like to mention, that there is the concept of summation of divergent series, assigning meaningful values for such expressions, for instance also for the "Euler-series" 1!x - 2!x^2 + 3!x^3 - 4!x^4 + ... - ... which has zero-radius of convergence as well. Using a summation-method based on Noerlund-means seem to allow to approximate values for fractional-iterations of exp(x)-1 which are consistent with the assumtion of additivity of iteration-heights

---

[update 24.2.2016]
I've a proposal for the growthrate of the coefficients in the power series for the half-iterate $d°^{0.5}(x) $ where $d(x) = \exp(x)-1$ .
Looking at the first 1024 coefficents $d_{k=0..1023} $ of this half-iterate it seems a sensical estimate $$a_{k=3..1023} = {2\over2^k}{ (k-3)! 3!\over (2 \pi)^k }$$ and $ c_k = { d_k \over a_k} $ seems to be bounded by inspection of that first 1024 coefficients (see the red horizontal line).
Moreover, the four partial sequences $ \{c_{4j}\} \; ,\; \{c_{4j+1} \} \; ,\; \{c_{4j+2} \} \; ,\; \{c_{4j+3}\} $ seem to have sinusoidal shape with frequency roughly depending on $ \log_2(k)$ .
Here is an image for that four partial sequences of the $ \{ c_k \} $: (in the picture I used $1/a_k$ instead of $a_k$ for the legend, sorry, I'll update that when I've time)

Pairs of sequences ($(c_0,c_2)$ and $(c_1,c_3)$) seem to be complementary in sign but completing in amplitude. Here is the picture, when the second sequence of one pair has the sign inverted:

---

Perhaps interestingly the "iterative logarithm" $\lambda(x)$ (or "logarithm of iteration" as named by G. Szekeres due to P. L. Walker (see below $[1]$) which is also resulting from the matrix-logarithm of the Carlemanmatrix for $d(x)$ ) has a very similar structure of divergent sequences of coefficients. Here is the analogue formula $ c_k ={ \lambda_k\over a_k}$ used and the four partial sequences graphed:

$[1]$ in Peter L. Walker, The exponential of iteration of $e^x-1$, Proc. Amer. Math. Soc. 110 (1990), no. 3, 611--620.)

---

[update 24.2.2016, 2] Here is a piece of code in Pari/GP whith which I could find the coefficients for the formal power series for $d° \,^{0.5}(x)$ (for 1024 terms used internal precision of 1200 digits and needed about 2200 sec. Only 0.5 sec for 128 terms, 1.5 sec for 256 terms where I used only lower precision of 200 and 400 internal digits respectively)

\\ Pari/GP
\\ make Carlemanmatrix D for d(x)=exp(x)-1
\\ and its squareroot D05 for d°0.5 (x)
\\ Coefficients for power series in 2nd column (D[,2],D05[,2])
\\ make D, D05 as global variables to avoid huge stack-allocation


{makemat_Dsqrt(dim=n,flg=1)=local(rs,cs); 
   \\ set flg = 1 (integer) for exact rational computation; DON'T for dim>128
   \\ set flg = 1.0 (real)  for real computation with "precision" digits

   D = matid(dim);rs=cs=dim; \\ set number of rows, cols from "dim"
   for(c=2,cs,
        for(r=c,rs,
              D[r,c] = flg *  (c-1)/(r-1)*(D[r-1,c-1] + D[r-1,c])
      ));

   D05=matrix(rs,cs,r,c,if(r==c,sqrt(D[r,r])));\\ this could simply be matid(dim)
   for(d=1,rs-1,
        for(r=d+1,rs,
             c=r-d;
             D05[r,c] = (D[r,c]-sum(k=c+1,r-1,D05[r,k]*D05[k,c]))
                       /(D05[c,c]+D05[r,r])
       ););
  return(Str("results are in global matrices D and D05, size ",rs,"x",cs));}
 \\============== end of routine ==========================================

default(realprecision,200);default(format,"g0.12")
gettime();print(makemat_Dsqrt(128,1.0));print(gettime()/1000.0," secs");
 \\ output:
 results are in global matrices D and D05, size 128x128
 0.562000000000 secs

default(realprecision,400);default(format,"g0.12")
gettime();print(makemat_Dsqrt(256,1.0));print(gettime()/1000.0," secs");
 \\ output:
 results are in global matrices D and D05, size 256x256
 1.54400000000 secs


default(realprecision,1200);default(format,"g0.12")
gettime();print(makemat_Dsqrt(1024,1.0));print(gettime()/1000.0," secs");
 \\ output:
 results are in global matrices D and D05, size 1024x1024
 2322.88700000 secs

Answer 9

And this is another construction.

Let $\sigma(x)=\exp(x)-1$ From this paper http://arxiv.org/abs/0812.4047 we know that

$$\exp(\sigma^{[p]}(t))=\sum_{n=0}^{\infty}B_n^p\frac{t^n}{n!}$$

where $B_n^p$ are the Bell's numbers of p-th order.

So to find $\sigma^{[1/2]}(t)$ we have to generalize Bell's numbers to fractional order. We can easily do that by induction as follows:

$$A_0^x=1$$ $$A_{n+1}^x=\sum_{k=0}^{x-1} A_n^x\star A_n^k$$

And then $$B_n^x=A_{n-1}^{x+1}$$

where $f(n)\star g(n)$ is the binomial convolution as described by Donald Knuth:

$$f(n)\star g(n)=\sum_{k=0}^n \binom nkf(n-k)g(k)$$

To obtain the value for any real x, we can note that the right part in $A_{n+1}^x=\sum_{k=0}^{x-1} A_n^x\star A_n^k$ is a polynomial of x and k of degree n-1 and integer coefficients and we can take indefinite sum of it symbolically following the rule

$$\sum_x ax^n=\frac{a B_{n+1}(x)}{n+1}$$

Where $B_a(x)$ are the Bernoulli polynomials.

Answer 10

Regarding the question

"Is this function f(x) or other functions with such an intermediate growth relevant to any interesting mathematics?"

you might be interested in the Grigorchuk group and other groups of intermediate growth.

Answer 11

Back on Scott Aaronson's blog, I gave an argument that $e^z+z-1$ should have an analytic compositional square root. The important difference between this function and $e^z-1$ was that the fixed point at $0$ has derivative $>1$, not $=1$. This should warn us that arguments based on the growth rate near infinity are inadequate. (Or else it should point out that my argument was broken!)

See comments below, my argument may have been broken. But, if so, I want to figure out why!

UPDATE: OK, I'm looking for some empirical data myself now. Let $e(z)=e^z+z-1$. My argument claimed that there should be an analytic and invertible $u$ (near 0) such that $u(e(z)) = 2 u(z)$. If such a $u$ exists, then $u^{-1}(2^{1/2} u(z))$ should have the desired property.

The nice thing about the equation $u(e(z)) = 2 u(z)$ is that it is linear in the coefficients of $u$. Here are the first 10 coefficients, computed with exact arithmetic.

{1, -(1/4), 1/18, -(1/96), 17/10800, -(47/267840), 4069/354352320, -(24907/102863416320), 475411/2893033584000, -(108314387/ 1314080143488000)}

And the numerical versions of the above

{1., -0.25, 0.0555556, -0.0104167, 0.00157407, -0.000175478, 0.0000114829, -2.42137*10^-7, 1.6433*10^-7, -8.2426*10^-8}

They seem to be converging rapidly.

Going a little further up, something odd happens. I computed the first 20 terms, of $u$, still using exact arithmetic, and I computed the ratios of successive terms. I'll just give you numeric data, because the fractions are huge.

{-0.25, -0.222222, -0.1875, -0.151111, -0.11148, -0.065438, -0.0210867, -0.678665, -0.50159, -0.155914, 0.12897, -0.691029, -0.153086, 0.158892, -0.657229, -0.165837, 0.119535, -0.806045, -0.191576}

So the ratios are usually small, but occasionally they jump up to larger than 0.5. That's still not evidence against convergence, but it suggests a need for caution (or the possibility of a bug!)

On the other hand, I also tried computing the $k$-th roots of successive terms, and the behavior was much smoother:

{1., 0.5, 0.381571, 0.319472, 0.275046, 0.236612, 0.196922, 0.148939, 0.176275, 0.195707, 0.191704, 0.185475, 0.205223, 0.200971, 0.197848, 0.213264, 0.210132, 0.203648, 0.218941, 0.217484}

Again, this is exact up until the point of taking a $k$-th root of a rational number.

UPDATE: Ok, I went and tried to repeat Ekhad's computation, and I think that Michael Lugo has found the error. Let $f(f(z)) = e^z+z-1$. I just did the first 5 terms, and I get:

Coefficients of $f$: {Sqrt[2], 1/4 (2 - Sqrt[2]), 1/36 (-9 + 7 Sqrt[2]), 1/288 (47 - 33 Sqrt[2]), (-4350 + 3071 Sqrt[2])/43200}

Table of $|f_i|^{1/i}$: {1.41421, 0.382683, 0.292347, 0.184117, 0.174302}

Table of $(i! |f_i|)^{1/i}$: {1.41421, 0.541196, 0.53123, 0.407517, 0.454086}

Notice that my second table, not my first, matches Ekhad. But my first table is the right thing to compute.

Answer 12

The following link and references contained therein might be of interest: http://www.math.niu.edu/~rusin/known-math/99/sqrt_exp

Answer 13

Non-convergence of the formal powerseries does not bother

Several times it was mentioned in the answers that the formal powerseries of the half iterate does not converge. That is true, however there is an elaborated theory about the fractional iteration of analytic functions with a fixed point $z_0$ which gives more far reaching answers.

Here we have the case of a parabolic fixpoint, i.e. $f'(z_0)=1$. These functions have mostly no fractional iterates analytic at the fixpoint.

But They have unique fractional iterates to the sides of the fixpoint, i.e. there are several domains bounded by/around the fixpoint which have the formal powerseries as asymptotic powerseries.

The arrangement of these domains is called Leau-Fatou flower (See the online book of Milnor [3] for details). The petals are alternating attractive and repellent when following the circle around the fixpoint. The number of these domains/petals is determined by number $m$ of zeros after the coefficient 1 in the powerseries development of $f$ at $z_0$. The number of domains is $2(m+1)$.

In our case the fixpoint is 0 and the development is $e^z-1=z+\frac{z^2}{2}+\dots$, so $m=0$ and the number of petals is 2. One petal (the repelling) is on the positive axis and one petal (the attracting) is on the negative axis. On these two petals (which overlap in the complex plane) are the two (different, not being analytic continuations) solutions defined, that have the formal powerseries as asymptotic powerseries.

There are several (general) formulas possible to numerically compute these two solutions.

The classic formula of Lévy for the Abel function (with $\alpha_u(u)=0$) is too slow for computations: $$\alpha_u(z) =\lim_{n\to\infty}\frac{f^{[n]}(z) - f^{[n]}(u)}{f^{[n+1]}(u)-f^{[n]}(u)} $$

The Newton formula for the regular fractional iteration is also too slow: $$f^{[t]}(z) = \sum_{n=0}^\infty \binom{t}{n} \sum_{m=0}^n \binom{n}{m} (-1)^{n-m} f^{[m]}(z)$$

But the following formulas for the Abel function (adapted to $f(x)=e^x-1$) are quickly converging: $$\alpha_1(z) = \lim_{n\to\infty} \frac{1}{3}\log(-f^{[n]}(z)) - \frac{2}{f^{[n]}(z)} - n, \quad z<0$$ $$\alpha_2(z) = \lim_{n\to\infty} \frac{1}{3}\log(f^{[-n]}(z)) - \frac{2}{f^{[-n]}(z)} + n, \quad z>0$$

You get the half iterate from the Abel function by $f^{[1/2]}(z)=\alpha^{-1}(1/2+\alpha(z))$ (independent on any additive constant of the Abel function). The non-Lévy formulas are probably first discovered by Écalle in his thesis [2] which deals completely with the parabolic case $f'(z_0)=1$.

[1] Kuczma, M., Choczewski, B., & Ger, R. (1990). Iterative functional equations. Encyclopedia of Mathematics and Its Applications, 32. Cambridge University Press.

[2] Écalle, J. (1974). Théorie des invariants holomorphes. Publications math'ematiques d'Orsay, 67-74 09. Orsay: Univ. Paris-XI.

[3] Milnor, J. (2006). Dynamics in one complex variable. 3rd ed. Princeton Annals in Mathematics 160. Princeton, NJ: Princeton University Press. viii, 304 p.

Answer 14

First, by the kindness of Daniel Geisler, I have a pdf of the graph of this, along with $ y = x$ and $ y = e^x - 1,$ at:

     (source)

The calculated function is analytic on the strictly positive real axis, analytic on the strictly negative real axis, and at least $C^1$ which applies only to behavior in the germ at the origin. Meanwhile, there is exactly one $C^1$ function that works, so this is it. The $C^1$ condition at $0$ is nothing more than the fact that the resulting function is between $x$ and $e^x-1,$ both for positive and negative $x.$ What I think is that the function is $C^\infty$ and the derivatives at $0$ are given by the formal power series solution. My hope is to prove, by basic methods, at least $C^8,$ as that is the approximation I use to graph near the origin. The method away from the origin is the same as that for sine, see

Does the formal power series solution to $f(f(x))= \sin( x) $ converge?

There are, however, a number of tweaks, as we actually need to work with the inverse function for $ x > 0,$ one must use a different branch of the logarithm for $x < 0,$ and so on. I am appending here a C++ program called abel.cc

which is compiled with

g++ -o abel abel.cc -lm

and then run with

./abel

#include <iostream.h>
#include <stdlib.h>
#include <fstream.h>
#include <sstream>
#include <list>
#include <set>
#include <math.h>
#include <iomanip.h>
#include <string>
#include <algorithm>
#include <iterator>
using namespace std;

// const int MINDISC =         27000;
// const int MAXDISC =         27000;

//   lines after double slashes are comments
//   also on a line with a command, anything after // is  commentary
//   on a Unix or Linux computer,  compile using line

//        g++ -o abel abel.cc -lm   

//  then run the program  with

//  ./abel  

double abel_positive(double x)
{
double eps = 0.000000001;
   eps /= 10000.0 ;    // satisfied at 10^{-14}
  double f = x ;
  double g = 1.0, g_old = 100.0, diff = 1.0 ;
 for( int n = 0; n <= 9000  && diff >= eps ; ++n)
 {
   g =  2 / f - log(f) / 3  + f / 36 - f * f / 540 - f * f * f / 7776 + 71 * f * f * f * f  /435456 - n ;
   diff = fabs(g - g_old);
//  cout.precision(16);
//   cout << n << "  " << x  << "  "  << f  << "  "  << g <<  "   " << diff << endl ;
   f = log ( 1.0 + f); 
   g_old = g;
 }
  return g;
}  // end  abel_positive


double abel_negative(double x)
{
double eps = 0.000000001;
   eps /= 10000.0 ;    // satisfied at 10^{-14}
  double f = x ;
  double g = 1.0, g_old = 100.0, diff = 1.0 ;
 for( int n = 0; n <= 1000  && diff >= eps ; ++n)
 {
   g =  2 / f - log(fabs(f)) / 3  + f / 36 - f * f / 540 - f * f * f / 7776 + 71 * f * f * f * f  /435456 + n ;
   g *= -1.0;
   diff = fabs(g - g_old);
//  cout.precision(16);
//   cout << n << " neg " << x  << "  "  << f  << "  "  << g <<  "   " << diff << endl ;
   f = exp (  f) - 1.0; 
   g_old = g;
 }
  return g;
}  // end  abel_negative

// alpha(x) = 2 / x - log(x) / 3  + x / 36 - x^2 / 540 - x^3 / 7776 + 71 * x^4 / 435456 - 8759 * x^5 / 163296000 - 31 * x^6 / 20995200


double inverse_abel_positive(double x)
{
  double eps = 0.000000001;
     eps /= 10000.0 ; //  satisfied at 10^{-14}
  double middle;
  if( x < -2.0001) return -5000000.0;
  else if ( x < -1.0001) return (  exp(inverse_abel_positive( x + 1.0)) - 1.0             );
  else
  {
    double left = 0.001, right = 200.0;
    middle = ( left + right) / 2.0; 
    double left_val = abel_positive(left) , right_val = abel_positive(right), middle_val = abel_positive(middle);
    while ( right - left > eps)
    {
      if (middle_val < x )
      {
        right = middle;
        middle = ( left + right) / 2.0;
         right_val = abel_positive(right);
        middle_val = abel_positive(middle);
      }
      else
      {
        left = middle;
        middle = ( left + right) / 2.0;
         left_val = abel_positive(left);
        middle_val = abel_positive(middle);
      }
    //  cout.precision(16);
    //  cout << middle << endl;
    } // while not accurate
  }  // else in range

  return  middle;
} //  end    inverse_abel_positive



double inverse_abel_negative(double x)
{
  double eps = 0.000000001;
     eps /= 10000.0 ; //  satisfied at 10^{-14}
  double middle;
  if( x < -2.0001) return -5000000.0;
  else if ( x < 1.04) return (  log(  1.0 + inverse_abel_negative( x + 1.0))             );
  else
  {
    double right = -0.01, left = -200.0;
    middle = ( left + right) / 2.0; 
    double left_val = abel_negative(left) , right_val = abel_negative(right), middle_val = abel_negative(middle);
    while ( right - left > eps)
    {
      if (middle_val > x )
      {
        right = middle;
        middle = ( left + right) / 2.0;
         right_val = abel_negative(right);
        middle_val = abel_negative(middle);    
      }
      else
      {
        left = middle;
        middle = ( left + right) / 2.0;
         left_val = abel_negative(left);
        middle_val = abel_negative(middle);
      }
   //   cout.precision(16);
   //   cout << middle << endl;
    } // while not accurate
  }  // else in range

  return  middle;
} //  end    inverse_abel_negative


double half_iterate(double x)
{
  if ( x > 0.1)  return inverse_abel_positive( -1/2.0 + abel_positive(x)  );
  else if ( x <= 0.1 && x >= -0.1 - 0.000000001 ) return x +  x * x / 4.0  +  x * x * x / 48.0   + x * x *  x * x * x / 3840.0  - 7 * x * x * x * x * x * x / 92160.0   +  x * x * x * x * x * x * x / 645120.0    + 53.0 * x * x * x * x * x * x * x * x / 3440640.0   ; // no x^4 term, it happens.
   else     return inverse_abel_negative( 1/2.0 + abel_negative(x)  );       
}  // half_iterate


//  gp pari :

// g = x + x^2 / 4 + x^3 /48 + x^5 / 3840 - 7 * x^6 / 92160 + x^7 / 645120 + 53 * x^8 /  3440640

// g + g^2 / 4 + g^3 / 48 + g^5 /  3840   - 7 * g^6 / 92160 + g^7 / 645120  + 53 * g^8 /  3440640

//  ...+ 488363/190253629440*x^13 + 5440363/713451110400*x^12 + 20071/1189085184*x^11 + 20971/825753600*x^10 + 971/46448640*x^9 + 1/40320*x^8 + 1/5040*x^7 + 1/720*x^6 + 1/120*x^5 + 1/24*x^4 + 1/6*x^3 + 1/2*x^2 + x


 //        g++ -o abel abel.cc -lm 

int main()
{

  for( double x = 5.4; x >= -3.45 ; x -= 0.01 )
  {

     cout.setf(ios::fixed, ios::floatfield);
     cout.precision(16);

//  cout << x << "    " << abel_positive( x) << "    "  << half_iterate( x) << "    "  << half_iterate(half_iterate( x)) << "    "  ;

// cout << x << "    " << abel_positive( x) << "    "  << half_iterate( x)  << "    "  ;


cout << x << "    "   << half_iterate( x)  << "    "  ;

cout.unsetf(ios::floatfield);
cout.unsetf(ios::fixed);
  cout.precision(4);
//cout << abel(log(1.0 + x)) - abel( x) - 1 << endl;
cout << half_iterate(half_iterate( x)) -  exp( x) + 1.0   << endl;

  }
  return 0 ;
}    //  end of main

 //        g++ -o abel abel.cc -lm   

Then I am appending the output, which is just the x value, the value of f(x), finally an error term f(f(x)) - exp(x) + 1. Actually, I had to give fewer outputs, there seems to be a size limit on computer output in MO.

phoebus:~/Cplusplus> ./abel
5.4000000000000004    16.3650724302248491    1.331e-09
5.3000000000000007    15.7879819196927205    2.847e-10
5.2000000000000011    15.2243680870229294    3.423e-10
5.1000000000000014    14.6740278132216613    1.348e-09
5.0000000000000018    14.1367598155454832    5.125e-10
4.9000000000000021    13.6123646385552366    -1.41e-10
4.8000000000000025    13.1006446447147358    3.756e-11
4.7000000000000028    12.6014040044095186    -2.856e-10
4.6000000000000032    12.1144486866975196    7.443e-10
4.5000000000000036    11.6395864499040993    -1.007e-10
4.4000000000000039    11.1766268322195632    6.662e-11
4.3000000000000043    10.7253811422648102    -3.654e-11
4.2000000000000046    10.2856624497240059    2.202e-10
4.1000000000000050    9.8572855759604447    8.681e-11
4.0000000000000053    9.4400670849610382    4.856e-10
3.9000000000000052    9.0338252736914679    -1.539e-10
3.8000000000000052    8.6383801632549879    1.661e-11
3.7000000000000051    8.2535534890740454    1.432e-11
3.6000000000000050    7.8791686923891451    -1.033e-10
3.5000000000000049    7.5150509103819285    1.846e-10
3.4000000000000048    7.1610269672691711    -3.851e-10
3.3000000000000047    6.8169253652572603    -1.32e-10
3.2000000000000046    6.4825762748621774    -2.01e-11
3.1000000000000045    6.1578115260938269    -8.575e-11
3.0000000000000044    5.8424645990524926    -1.462e-11
2.9000000000000044    5.5363706146241647    1.361e-11
2.8000000000000043    5.2393663251515896    -2.929e-12
2.7000000000000042    4.9512901050766569    -4.294e-11
2.6000000000000041    4.6719819413692445    -1.235e-11
2.5000000000000040    4.4012834240498844    2.79e-11
2.4000000000000039    4.1390377362686763    -2.539e-11
2.3000000000000038    3.8850896444937177    -1.616e-13
2.2000000000000037    3.6392854882807599    4.231e-12
2.1000000000000036    3.4014731698489813    3.428e-12
2.0000000000000036    3.1715021431943606    6.262e-13
1.9000000000000035    2.9492234028327093    2.941e-12
1.8000000000000034    2.7344894719531982    1.509e-11
1.7000000000000033    2.5271543897887909    1.412e-13
1.6000000000000032    2.3270736982303024    1.964e-12
1.5000000000000031    2.1341044271723417    -9.805e-13
1.4000000000000030    1.9481050786134744    -4.962e-12
1.3000000000000029    1.7689356089101538    1.714e-13
1.2000000000000028    1.5964574088813634    -1.159e-12
1.1000000000000028    1.4305332811341520    -1.013e-12
1.0000000000000027    1.2710274138894109    7.816e-13
0.9000000000000027    1.1178053503667034    -1.945e-13
0.8000000000000027    0.9707339525168228    -3.206e-13
0.7000000000000027    0.8296813575533253    3.708e-13
0.6000000000000028    0.6945169252836292    2.309e-14
0.5000000000000028    0.5651111736539647    -1.235e-13
0.4000000000000028    0.4413356992547828    -3.93e-13
0.3000000000000028    0.3230630786173595    -1.743e-14
0.2000000000000028    0.2101667451936166    2.259e-14
0.1000000000000028    0.1025208358618962    8.632e-14
0.0000000000000028    0.0000000000000028    -8.327e-17
-0.0999999999999972    -0.0975208360134532    -1.577e-14
-0.1999999999999972    -0.1901667548369642    1.416e-14
-0.2999999999999972    -0.2780631873408490    5.551e-15
-0.3999999999999972    -0.3613363013525148    5.274e-14
-0.4999999999999972    -0.4401134277164546    -4.774e-14
-0.5999999999999972    -0.5145235016776626    -2.472e-13
-0.6999999999999972    -0.5846974891233467    1.36e-14
-0.7999999999999972    -0.6507687621527771    -4.419e-14
-0.8999999999999971    -0.7128733880168525    1.32e-13
-0.9999999999999971    -0.7711502997203856    -1.19e-13
-1.0999999999999972    -0.8257413246049203    3.442e-15
-1.1999999999999973    -0.8767910576263940    1.829e-13
-1.2999999999999974    -0.9244465773015511    -3.32e-14
-1.3999999999999975    -0.9688570130908518    -2.05e-13
-1.4999999999999976    -1.0101729822279837    -2.889e-14
-1.5999999999999976    -1.0485459210648198    2.558e-13
-1.6999999999999977    -1.0841273405174991    -2.204e-13
-1.7999999999999978    -1.1170680371664736    5.618e-14
-1.8999999999999979    -1.1475172912584388    -7.605e-15
-1.9999999999999980    -1.1756220805208741    -3.389e-14
-2.0999999999999979    -1.2015263350700924    4.802e-15
-2.1999999999999980    -1.2253702540044693    3.331e-13
-2.2999999999999980    -1.2472896992571449    -3.854e-13
-2.3999999999999981    -1.2674156771038474    1.388e-13
-2.4999999999999982    -1.2858739130575336    -8.189e-13
-2.5999999999999983    -1.3027845214953375    -1.961e-13
-2.6999999999999984    -1.3182617679403474    -1.768e-14
-2.7999999999999985    -1.3324139189760200    -1.3e-14
-2.8999999999999986    -1.3453431728233207    -1.149e-14
-2.9999999999999987    -1.3571456621162299    -8.366e-14
-3.0999999999999988    -1.3679115197319236    7.921e-14
-3.1999999999999988    -1.3777249981938211    1.012e-14
-3.2999999999999989    -1.3866646333660464    2.682e-13
-3.3999999999999990    -1.3948034435566479    -6.27e-13
phoebus:~/Cplusplus>

Answer 15

Here is light-hearted Mathematica holiday gift for everyone who has ever wondered (as I have) whether (smooth) half-exponential functions exist, and if so, what their graphs look like.

The short answer is, yes, half-exponential functions do exist ... and their graphs look pretty much as we might (in retrospect) expect. Be advised, however, that the Mathematica notebook linked-to above uses engineering-grade mathematical methods (meaning, fans of rigor may be disappointed).

The key idea is to specify the half-exponential composition relation as f(f(x)) = α exp(x-α), where α is an arbitrary real constant; this provides a starting fixed-point identity f(α)=α. The rest of the construction is straightforward: we construct a series expansion about this fixed point, then Padé-approximate the series (to expand its convergence radius).

Needless to say, this approach tells us nothing about the analytic structure of f ... but the numerical robustness of the above Padé construction hints that a general integral representation for f (for example) might possibly be found.

If for some reason anyone needs a concrete numerical instantiation of a half-exponential function, these Padé methods might perhaps be useful ... my own motivation was pure fun.

Happy Holidays to everyone! :)