Is this an instance of the snake lemma?

Question

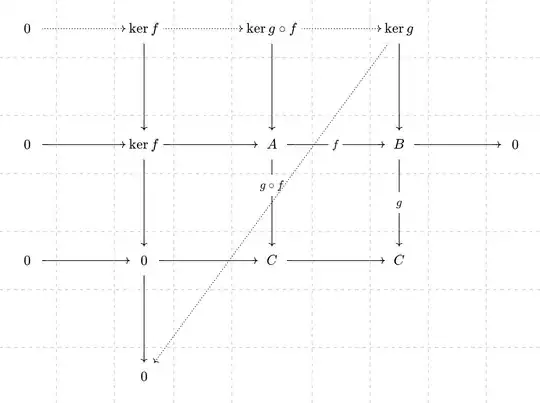
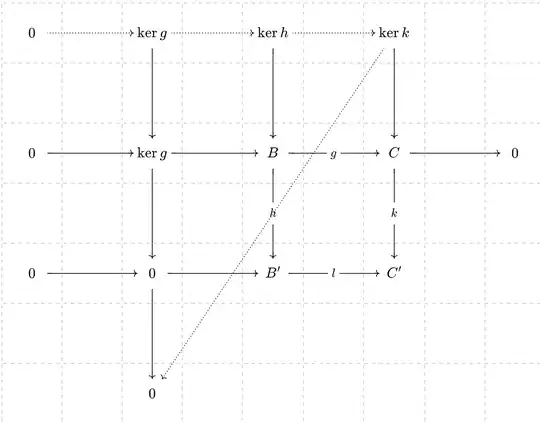
I recently had need of the following fact (in the category of abelian groups, but I'm pretty sure it holds for all abelian categories): given a commutative diagram of the form

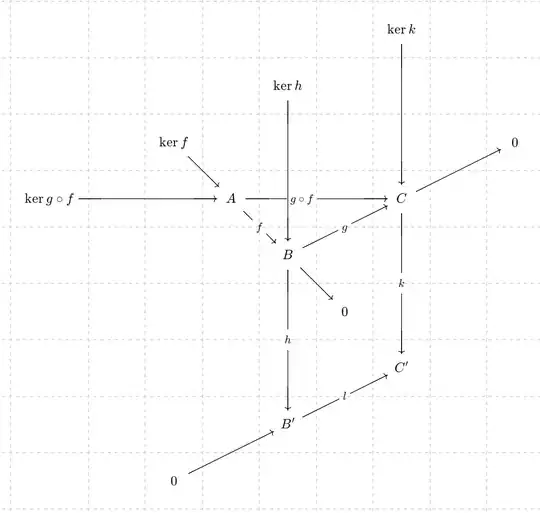(quiver link), thus $k \circ g = l \circ h$, $f$ and $g$ are epimorphisms, and $l$ is a monomorphism, there is a canonical long exact sequence $$ 0 \to \ker f \to \ker g \circ f \to \ker h \to \ker k \to 0$$ defined in a natural fashion. Verifying that this fact is a routine (but tedious) diagram chase. Given the similarity to the snake lemma, I was initially certain that this fact was somehow a corollary of the snake lemma, but I was only able to use the snake lemma to establish exactness at $\ker k$ and nowhere else. Can the entirety of this sequence be established from the snake lemma, or one of the other canonical diagram chase lemmas?

EDIT: As noted in comments, the claim follows in fact from splicing together two applications of the snake lemma, namely

and

This kind of inquiry seems to beg the question: can every diagram chase lemma be formally derived from the "canonical" ones (snake, five, nine, etc.)? I don't even know if this question can be made precise though. — R.P., Dec 23 '23 at 23:05
@R.P. One thing to keep in mind is that diagram chasing as a decision problem (once properly defined!) is undecidable. This at least puts a damper on hoping for too much. — Carl-Fredrik Nyberg Brodda, Dec 23 '23 at 23:07
@Carl-FredrikNybergBrodda Rats. But thank you for this useful bit of perspective. — R.P., Dec 23 '23 at 23:08
@Carl-FredrikNybergBrodda is it because deciding upon diagram chasing (whatever it means: does it mean "tell whether $f=g$ for two parallel morphisms of a category"?) would imply deciding on the word problem for groups? — fosco, Dec 24 '23 at 09:32
@fosco Semigroups, but yes, that’s the idea. The reference is G. Hutchinson: Recursively unsolvable word problems of modular lattices and diagram-chasing, J. Algebra 26 (1973), 385--399 (John Stillwell showed me this beautiful paper). — Carl-Fredrik Nyberg Brodda, Dec 24 '23 at 09:46
@R.P.: See also the discussion in this question: https://mathoverflow.net/questions/12732/is-the-theory-of-categories-decidable — aorq, Dec 25 '23 at 02:25

John Rognes · Accepted Answer · 2023-12-23T23:50:39.433

21

Splice the left ends of the kernel-cokernel exact sequences $0 \to \ker(f) \to \ker(gf) \to \ker(g) \to \mathrm{cok}(f) \to \mathrm{cok}(gf) \to \mathrm{cok}(g) \to 0$ and $0 \to \ker(g) \to \ker(kg) \to \ker(k) \to \mathrm{cok}(g) \to \mathrm{cok}(kg) \to \mathrm{cok}(k) \to 0$, noting that $\ker(kg) = \ker(h)$, $\mathrm{cok}(f) = 0$ and $\mathrm{cok}(g) = 0$. The kernel-cokernel sequence for a composition appears in Milne's Arithmetic Duality Theorems (Proposition 0.24), Short exact sequences every mathematician should know and https://arxiv.org/abs/2001.07528 , but must be about as old as the snake lemma.

edited Dec 23 '23 at 23:50

answered Dec 23 '23 at 21:33

John Rognes

8,692

3

First time I saw the kernel-cokernel sequence is Proposition 4.5 (on page 25) in "Algebraic K-theory" by Bass. It is from 1968. Bass does not refer to anything there. It still might be older though. – მამუკა ჯიბლაძე Dec 23 '23 at 21:49
7

Not a historical comment, but this is an instance of the octahedral lemma, yes? – mme Dec 23 '23 at 21:50
5

Thanks! It surprises me that there are two fundamental diagram chase lemmas concerning the kernel and cokernel of maps, but that one of them is substantially more famous than the other... I had never encountered the kernel-cokernel exact sequence before, but have been exposed to the snake lemma countless times. – Terry Tao Dec 23 '23 at 22:02
1

Though in this particular case it looks like the short exact sequences $0 \to \mathrm{ker}(f) \to \mathrm{ker}(gf) \to \mathrm{ker}(g) \to 0$ and $0 \to \mathrm{ker}(g) \to \mathrm{ker}(h) \to \mathrm{ker}(k) \to 0$ could also be derived directly from the snake lemma. – Terry Tao Dec 23 '23 at 22:03
4

@TerryTao: On pg. 2 of the linked arXiv preprint of Rui Xiong it looks like the kernel-cokernel exact sequence is proved using the snake lemma. – Sam Hopkins Dec 23 '23 at 22:06
4

@SamHopkins OK, that partially explains why the snake lemma is more widely known. Still, I would have thought that the kernel cokernel exact sequence should at least merit a Wikipedia entry or something. – Terry Tao Dec 23 '23 at 22:32
7

Both the snake lemma and the kernel-cokernel sequence are instances of the long exact sequence of homotopy groups induced by a fiber sequence of anima, which is really the fundamental thing that is the source of almost all long exact sequences. For the snake lemma, the relevant fiber sequence is the fiber of a map of fiber sequences, while for the kernel-cokernel sequence, it is the fiber sequence of fibers of a commuting triangle (the "octahedral axiom" as mentioned by mme). – Marc Hoyois Dec 24 '23 at 08:47
1

@Marc Hoyois: the first sentence of your comment sounds like a parody of the worst tendencies of hotopically minded people. – Satan's Minion Dec 26 '23 at 14:51
4

@Satan'sMinion that’s rather too much pearl-clutching for a mathematician observing that two things are both instances of one more general thing, especially after another mathematician explicitly expressed surprise that there should be two such different but similar things. – Kevin Carlson Dec 27 '23 at 14:51

Is this an instance of the snake lemma?

1 Answers1